题目内容
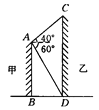
【题目】如图所示,两建筑物的水平距离为24 m,从A点测得D点的俯角为60°,测得C点的仰角为40°,求这两座建筑物的高.(![]() ≈1.732,tan 40°≈0.8391,精确到0.01 m)
≈1.732,tan 40°≈0.8391,精确到0.01 m)
【答案】61.7l m
【解析】试题分析:过点A作AE⊥CD于点E,可得四边形ABDE为矩形,AB=ED,BD=AE,然后在Rt△AED和Rt△AEC中,分别求出DE和EC的长度,继而可求得建筑物CD的高度和建筑物AB的高度.
试题解析:作AE⊥CD于E,

则AE=BD=24m,
在Rt△AED中,tan∠DAE=![]() ,
,
∴DE=AEtan 60°≈24×1.732≈41.57(m),
∴AB=DE≈41.57(m).
在Rt△AEC中,tan∠CAE=![]() ,
,
∴CE=AEtan 40°≈24×0.8391≈20.14(m),
∴CD=CE+DE≈20.14+41.57=61.71(m),
∴甲建筑物的高AB约为41.57 m,乙建筑物的高CD约为61.7l m.

【题目】为了丰富学生校园生活,满足学生的多元文化需求,促进学生身心健康和谐发展,学校开展了丰富多彩的社团活动.我区某中学开展的社团活动有:A.尤克里里、B.街舞、C.羽毛球、D.口琴、E.沙画.学生管理中心为了了解全校800名学生的社团需求,开展了一次调查研究,请将下面的调查过程补全.
抽样调查:学生管理中心计划选取40名学生进行问卷调查,下面的抽样方法中, 合理的是 (填序号);
①从七、八、九三个年级中随机抽取40名女生进行问卷调查;
②从七、八、九三个年级中随机抽取男、女生共40名进行问卷调查.
收集数据:抽样方法确定后,学生管理中心收集到如下数据(社团项目的编号,用字母代号表示)
B,E,B,A,E,C,C,C,B,B
A,C,E,D,B,A,B,E,C,A
D,D,B,B,C,C,A,A,E,B
C,B,D,C,A,C,C,A,C,E
整理、描述数据:划记、整理、描述样本数据、绘制统计图如下,请补全统计表和统计图.
选择各社团项目的人数统计表
社团项目 | 划记 | 人数 |
A尤克里里 | 正 | 8 |
B街舞 | ||
C羽毛球 | 正正丅 | 12 |
D口琴 | ||
E沙画 | 正一 | 6 |
合计 | 40 | 40 |

分析数据、推断结论:
(1)在扇形统计图中,“B街舞”所在的扇形的圆心角等于 度;
(2)根据学生管理中心获得的样本数据估计全校大约有多少名同学选择羽毛球这个社团?






