题目内容
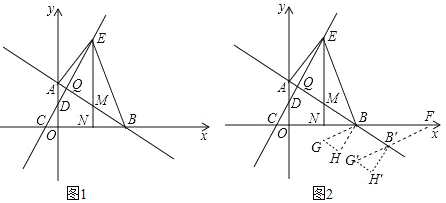
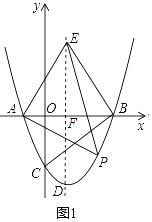
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,过点B作BC的垂线,交对称轴于点E.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,过点B作BC的垂线,交对称轴于点E.

(1)求证:点E与点D关于x轴对称;
(2)点P为第四象限内的抛物线上的一动点,当△PAE的面积最大时,在对称轴上找一点M,在y轴上找一点N,使得OM+MN+NP最小,求此时点M的坐标及OM+MN+NP的最小值;
(3)如图2,平移抛物线,使抛物线的顶点D在射线AD上移动,点D平移后的对应点为D′,点A的对应点A′,设抛物线的对称轴与x轴交于点F,将△FBC沿BC翻折,使点F落在点F′处,在平面内找一点G,若以F′、G、D′、A′为顶点的四边形为菱形,求平移的距离.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() ,
, ![]() ,
, ![]()
【解析】试题分析:(1)首先求出A、B、C、D的坐标,再根据△EFB∽△BOC对应边成比例得出方程,推出EF的长度,求出点E的坐标即可解决问题;
(2)过点P作PQ∥y轴,交直线AE于点Q.构建 二次函数,利用二次函数的性质求出点P的坐标,作点O关于对称轴的对称点O′,作点P关于Y轴的对称点P′,连接O′P′,分别交对称轴、y轴于点M、N,此时M、N即为所求;
(3)由题意得F,A,D三点的坐标,设平移距离为![]() t,则得出A′,D′的坐标,可得A′F2,D′F′2,,A′D′2的长度,然后分三种情形:①当A′F2=D′F′2时,②当A′F′2=A′D′2时,③当D′F′2=A′D′2时列出方程即可解决问题.
t,则得出A′,D′的坐标,可得A′F2,D′F′2,,A′D′2的长度,然后分三种情形:①当A′F2=D′F′2时,②当A′F′2=A′D′2时,③当D′F′2=A′D′2时列出方程即可解决问题.
试题解析:解:(1)如图1中,令y=0,得到![]() x2﹣
x2﹣![]() x﹣3=0,解得x=﹣
x﹣3=0,解得x=﹣![]() 或3
或3![]() ,∴A(﹣
,∴A(﹣ ![]() ,0),B(3
,0),B(3 ![]() ,0).
,0).
令x=0,可得y=﹣3,∴C(0,﹣3).
∵y= ![]() x2﹣
x2﹣ ![]() x﹣3=
x﹣3=![]() (x﹣
(x﹣ ![]() )2﹣4,∴顶点D(
)2﹣4,∴顶点D( ![]() ,﹣4),设对称轴与x轴交于F,则BF=2
,﹣4),设对称轴与x轴交于F,则BF=2 ![]() .
.
∵△EFB∽△BOC,∴ EF:OB=BF:OC,∴ ![]() ,∴EF=4,∴E(
,∴EF=4,∴E( ![]() ,4),∴E、D关于x轴对称;
,4),∴E、D关于x轴对称;
(2)过点P作PQ∥y轴,交直线AE于点Q.
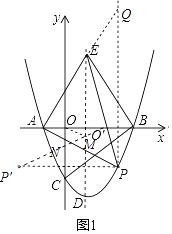
∵yAE= ![]() x+2,∴设P(a,
x+2,∴设P(a, ![]() a2﹣
a2﹣![]() a﹣3),Q(a,
a﹣3),Q(a, ![]() a+2),(0<a<3
a+2),(0<a<3![]() ),∴PQ=(
),∴PQ=(![]() a+2)﹣(
a+2)﹣(![]() a2﹣
a2﹣![]() a﹣3)=﹣
a﹣3)=﹣![]() a2+2
a2+2 ![]() a+5,∴S△PAE=
a+5,∴S△PAE= ![]() PQ|xE﹣xA|=
PQ|xE﹣xA|= ![]() (﹣
(﹣![]() a2+2
a2+2![]() a+5)2
a+5)2![]() =﹣
=﹣![]() a2+4a+5
a2+4a+5![]() ,∴当a=
,∴当a=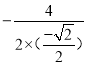 =2
=2![]() 时,S△PAE最大,此时P(2
时,S△PAE最大,此时P(2![]() ,﹣3).
,﹣3).
作点O关于对称轴的对称点O′(2![]() ,0),作点P关于Y轴的对称点P′(﹣2
,0),作点P关于Y轴的对称点P′(﹣2![]() ,﹣3).连接O′P′,分别交对称轴、y轴于点M、N,此时M、N即为所求.
,﹣3).连接O′P′,分别交对称轴、y轴于点M、N,此时M、N即为所求.
∴yP′O′=![]() x﹣
x﹣![]() ,当x=
,当x=![]() 时,y=﹣
时,y=﹣![]() ,∴M(
,∴M(![]() ,﹣
,﹣![]() ),∴OM+MN+NP的最小值O′P′=
),∴OM+MN+NP的最小值O′P′=![]() =
= ![]() ;
;
(3)∵F′(![]() ,﹣
,﹣![]() ),A(﹣
),A(﹣![]() +
+![]() t,﹣2t),D(
t,﹣2t),D(![]() ,﹣4),
,﹣4),
设平移距离为 ![]() t,则A′(﹣
t,则A′(﹣ ![]() +
+ ![]() t,﹣2t),D′(
t,﹣2t),D′( ![]() +
+![]() t,﹣4﹣2t),
t,﹣4﹣2t),
A′F2=6t2﹣24t+![]() ,D′F′2=6t2+
,D′F′2=6t2+![]() ,A′D′2=24,
,A′D′2=24,
①当A′F2=D′F′2时,6t2﹣24t+ ![]() =6t2+
=6t2+![]() ,解得t=1.
,解得t=1.
②当A′F′2=A′D′2时,6t2﹣24t+ ![]() =24,解得t=
=24,解得t=![]() .
.
③当D′F′2=A′D′2时,24=6t2+ ![]() ,解得t=
,解得t=![]() 或﹣
或﹣![]() (舍弃),
(舍弃),
∴平移的距离![]() t=
t= ![]() ,
, ![]() ,
, ![]() .
.

 计算高手系列答案
计算高手系列答案【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

【题目】某班“数学兴趣小组”对函数y=|x|-2的图象特征进行了探究,探究过程如下:
⑴自变量x的取值范围是全体实数,x与y的几组对应值如下:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 1 | m | -1 | -2 | n | 0 | 1 | 2 | … |
其中,m= ,n= .
⑵根据表中数据,在如图所示的平面直角坐标系中描点,并画出函数图象;

⑶观察函数图象,写出一条特征: .