��Ŀ����
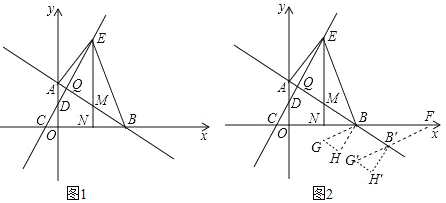
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��AB��y�ύ�ڵ�![]() ����x�ύ�ڵ�B��
����x�ύ�ڵ�B��![]() ��ֱ��CD��y�ύ�ڵ�D����x�ύ�ڵ�
��ֱ��CD��y�ύ�ڵ�D����x�ύ�ڵ�![]() ��
��![]() ��ֱ��AB��ֱ��CD���ڵ�Q��EΪֱ��CD��һ���㣬����E��x��Ĵ��ߣ���ֱ��AB�ڵ�M����x���ڵ�N������AE��BE��
��ֱ��AB��ֱ��CD���ڵ�Q��EΪֱ��CD��һ���㣬����E��x��Ĵ��ߣ���ֱ��AB�ڵ�M����x���ڵ�N������AE��BE��
![]() ��ֱ��AB��CD�Ľ���ʽ����Q�����ꣻ
��ֱ��AB��CD�Ľ���ʽ����Q�����ꣻ
![]() ��E���˶���Q����Ҳ࣬��
��E���˶���Q����Ҳ࣬��![]() �����Ϊ
�����Ϊ![]() ʱ����y������һ����P��ֱ��AB����һ����R����
ʱ����y������һ����P��ֱ��AB����һ����R����![]() ���ܳ���Сʱ�����P�����꼰
���ܳ���Сʱ�����P�����꼰![]() �ܳ�����Сֵ��
�ܳ�����Сֵ��
![]() ��
��![]() �ʵ������£���ͼ2��
�ʵ������£���ͼ2��![]() ���ŵ�B��ʱ����ת
���ŵ�B��ʱ����ת![]() �õ�
�õ�![]() ��ʹ��M���G�غϣ���N���H�غϣ��ٽ�
��ʹ��M���G�غϣ���N���H�غϣ��ٽ�![]() ����ֱ��ABƽ�ƣ���ƽ���е�
����ֱ��ABƽ�ƣ���ƽ���е�![]() Ϊ
Ϊ![]() ����ƽ�ƹ����У���ֱ��
����ƽ�ƹ����У���ֱ��![]() ��x�ύ�ڵ�F���Ƿ���������ĵ�F��ʹ��
��x�ύ�ڵ�F���Ƿ���������ĵ�F��ʹ��![]() Ϊ���������Σ������ڣ������ʱ��F�����ꣻ�������ڣ�˵������
Ϊ���������Σ������ڣ������ʱ��F�����ꣻ�������ڣ�˵������
���𰸡���1����Q����Ϊ![]() ����2��
����2��![]() �ܳ�����Сֵ����СֵΪ
�ܳ�����Сֵ����СֵΪ![]() ����3����F������Ϊ
����3����F������Ϊ![]() ��
��
��������
![]() ��ֱ��CD����ʽ��kֵΪ
��ֱ��CD����ʽ��kֵΪ![]() ���������ֱ��CD�ı���ʽ��ͬ���ɵ�ֱ��AB�ı���ʽ��������������ʽ����������Q�����ꣻ
���������ֱ��CD�ı���ʽ��ͬ���ɵ�ֱ��AB�ı���ʽ��������������ʽ����������Q�����ꣻ
![]() �������N���ꣻ��N��������ԳƵ�
�������N���ꣻ��N��������ԳƵ�![]() ��
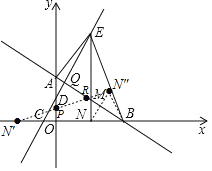
��![]() ������
������![]() ��AB�ڵ�R��y���ڵ�P����ʱ��
��AB�ڵ�R��y���ڵ�P����ʱ��![]() �ܳ�����Сֵ����⼴�ɣ�
�ܳ�����Сֵ����⼴�ɣ�
![]() �ǵ�Ϊ
�ǵ�Ϊ![]() �ĵ��������Σ�
�ĵ��������Σ�![]() Ϊ���������Σ�������⣮
Ϊ���������Σ�������⣮
![]() ��
��![]() ��
��![]() ��
��![]() ��ֱ��CD����ʽ��kֵΪ
��ֱ��CD����ʽ��kֵΪ![]() ��
��
��ֱ��CD�ı���ʽΪ��![]() ������C���������ʽ����ã�
������C���������ʽ����ã�![]() ��
��
�ʣ�ֱ��CD�ı���ʽΪ��![]() ��
��
ͬ���ɵ�ֱ��AB�ı���ʽΪ��![]() ��
��![]() ��
��
����![]() ����ã�
����ã�![]() ������Q����Ϊ
������Q����Ϊ![]() ��
��
![]() ��ͼ��ʾ�����E������Ϊ
��ͼ��ʾ�����E������Ϊ![]() �����
�����![]() ��
��
![]() ��
��
��ã�![]() ������N����Ϊ
������N����Ϊ![]() ����
����![]() ��
��
����N����ֱ��AB��y��ĶԳƵ�![]() ��
��![]() ������
������![]() ��AB�ڵ�R��y���ڵ�P��
��AB�ڵ�R��y���ڵ�P��
��ʱ��![]() �ܳ�����Сֵ����СֵΪ��
�ܳ�����Сֵ����СֵΪ��![]() �ij��ȣ�
�ij��ȣ�
![]() ��
��![]() ����ֱ��AB�Գƣ�
����ֱ��AB�Գƣ�![]() ��
��
![]() Ϊ�߳�Ϊ3�ĵȱ������Σ������θ�Ϊ��
Ϊ�߳�Ϊ3�ĵȱ������Σ������θ�Ϊ��![]() ��
��
���![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��
��ֱ��![]() �ı���ʽΪ��
�ı���ʽΪ��![]() ������P����
������P����![]() ��
��
![]() �ܳ�����Сֵ����СֵΪ
�ܳ�����Сֵ����СֵΪ![]() ��
��
![]() ��ͼ2����
��ͼ2����![]() ���ŵ�B��ʱ����ת
���ŵ�B��ʱ����ת![]() �õ�
�õ�![]() ��
��
��ʱ![]() ������GM����x��Գƣ����
������GM����x��Գƣ����![]() ��
��![]() ��
��
ͼ��ƽ��Ϊ![]() ʱ��
ʱ��![]() ��
��
��![]() �ǵ�Ϊ
�ǵ�Ϊ![]() �ĵ��������Σ���
�ĵ��������Σ���![]() Ϊ���������Σ�ֻ��
Ϊ���������Σ�ֻ��![]() ��
��
![]() ��
��![]() ��
��
�ʵ�F������Ϊ![]() ��
��



