题目内容
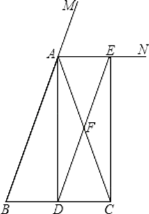
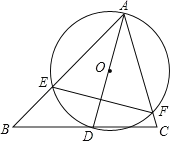
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的一个动点,以
上的一个动点,以![]() 为直径作
为直径作![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() ,当线段
,当线段![]() 长度取最小值时,
长度取最小值时,![]() ______.
______.
【答案】![]()
【解析】
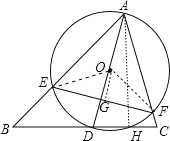
连结OE、OF,作OG⊥EF于G,AH⊥BC于H,如图,设⊙O的半径为r,易得△ABH为等腰直角三角形,则可求出AH的长,根据三角形内角和计算出∠BAC=60°,于是根据圆周角定理得到∠EOF=2∠BAC=120°,则∠OEF=30°,接着根据垂径定理得EG=FG,然后根据含30度的直角三角形三边的关系得到EG=![]() OG=
OG=![]() r,则EF=2EG=
r,则EF=2EG=![]() r,由于AD为⊙O的直径,利用垂线段最短得AD=AH=6时,AD最短,半径最小,EF最小,此时CD=CH,接着利用75°的正切值求出CH,从而得到CD的长.
r,由于AD为⊙O的直径,利用垂线段最短得AD=AH=6时,AD最短,半径最小,EF最小,此时CD=CH,接着利用75°的正切值求出CH,从而得到CD的长.
连结OE、OF,作OG⊥EF于G,AH⊥BC于H,如图,设⊙O的半径为r.
∵∠ABC=45°,∴△ABH为等腰直角三角形,∴AH=![]() AB=
AB=![]() ×6
×6![]() =6.
=6.
∵∠BCA=75°,∠ABC=45°,∴∠BAC=180°﹣75°﹣45°=60°,∴∠EOF=2∠BAC=120°.
∵OE=OF,∴∠OEF=30°.
∵OG⊥EF,∴EG=FG.在Rt△OEG中,OG=![]() OE=
OE=![]() r,∴EG=
r,∴EG=![]() OG=
OG=![]() r,∴EF=2EG=
r,∴EF=2EG=![]() r.
r.
∵AD为⊙O的直径,∴当AD=AH=6时,AD最短,半径最小,EF最小,此时CD=CH.在Rt△ACH中,tan∠ACH=tan75°=![]() =2+
=2+![]() ,∴CH=
,∴CH=![]() =
=![]() ,∴此时CD的长为
,∴此时CD的长为![]() .
.
故答案为:![]() .
.

【题目】某商品的进价为每件20元,售价为每件30元,每月可卖出180件,如果该商品计划涨价销售,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数)时,月销售利润为y元.
(1)分析数量关系填表:
每台售价(元) | 30 | 31 | 32 | …… | 30+x |
月销售量(件) | 180 | 170 | 160 | …… | _____ |
(2)求y与x之间的函数解析式和x的取值范围
(3)当售价x(元/件)定为多少时,商场每月销售这种商品所获得的利润y(元)最大?最大利润是多少?