题目内容
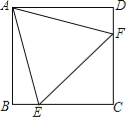
【题目】如图，在△ABC中，AB＝AC，AD⊥BC垂足是D，AN是∠BAC的外角∠CAM的平分线，CE⊥AN，垂足是E，连接DE交AC于F．
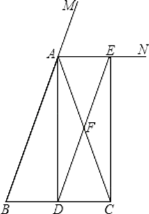
（1）求证：四边形ADCE为矩形；
（2）求证：DF∥AB，DF＝
；
（3）当△ABC满足什么条件时，四边形ADCE为正方形，简述你的理由．
【答案】（1）见解析；（2）见解析；（3）当△ABC是等腰直角三角形时，四边形ADCE为正方形．见解析
【解析】
（1）先根据AB=AC，AD⊥BC垂足是D，得AD平分∠BAC，然后根据AE是△ABC的外角平分线，可求出AN∥BC，故∠DAE=∠ADC=∠AEC=90°，所以四边形ADCE为矩形；
（2）根据四边形ADCE是矩形，可知F是AC的中点，由AB=AC，AD平分∠BAC可知D是BC的中点，故DF是△ABC的中位线，即DF∥AB，DF=
AB；
（3）根据矩形的性质可知当△ABC是等腰直角三角形时，则∠5=∠2=45°，利用等腰三角形的性质定理可知对应边AD=CD．再运用邻边相等的矩形是正方形．问题得证．
证明：如图
（1）∵AB＝AC，AD⊥BC垂足是D，
∴AD平分∠BAC，∠B＝∠5，
∴∠1＝∠2，
∵AE是△ABC的外角平分线，
∴∠3＝∠4，
∵∠1+∠2+∠3+∠4＝180°，
∴∠2+∠3＝90°，
即∠DAE＝90°，
又∵AD⊥BC，
∴∠ADC＝90°，
又∵CE⊥AE，
∴∠AEC＝90°，
∴四边形ADCE是矩形．
（2）∵四边形ADCE是矩形，
∴AF＝CF＝AC，
∵AB＝AC，AD平分∠BAC，
∴BD＝CD＝BC，
∴DF是△ABC的中位线，
即DF∥AB，DF＝
．
（3）当△ABC是等腰直角三角形时，四边形ADCE为正方形．
∵在Rt△ABC中，AD平分∠BAC
∴∠5＝∠2＝∠3＝45°，
∴AD＝CD，
又∵四边形ADCE是矩形，
∴矩形ADCE为正方形．
