Question

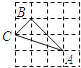
【题目】已知：如图，△ABC是等边三角形，点D、E分别在边BC、AC上，∠ADE=60°．

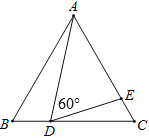
（1）求证：△ABD∽△DCE；

（2）如果AB=3，EC=，求DC的长．

Answer 1

【答案】（1）见解析；（2）DC=1或DC=2．

【解析】

试题分析：（1）△ABC是等边三角形，得到∠B=∠C=60°，AB=AC，推出∠BAD=∠CDE，得到△ABD∽△DCE；

（2）由△ABD∽△DCE，得到=，然后代入数值求得结果．

（1）证明：∵△ABC是等边三角形，

∴∠B=∠C=60°，AB=AC，

∵∠B+∠BAD=∠ADE+∠CDE，∠B=∠ADE=60°，

∴∠BAD=∠CDE

∴△ABD∽△DCE；

（2）解：由（1）证得△ABD∽△DCE，

∴=，

设CD=x，则BD=3﹣x，

∴=，

∴x=1或x=2，

∴DC=1或DC=2．