题目内容
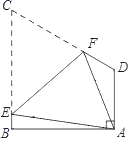
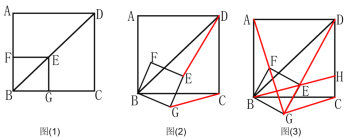
【题目】如图(1),已知点E在正方形ABCD的对角线BD上,EG⊥BC,垂足为点G,EF⊥AB,垂足为点F.
(1)证明与猜想:
①求证:△BEF∽△BDA;
②猜想:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形BFEG绕点B顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段DE与CG之间的数量关系,并说明理由;
(3)拓展与运用:正方形BFEG在旋转过程中,当A,F,G三点在一条直线上时,如图(3)所示,延长BE交CD于点H.若DE=3,EH=![]() ,则BC= .
,则BC= .
【答案】(1) ①证明如下,②![]() .(2)DE=
.(2)DE=![]() CG (3)
CG (3)![]()
【解析】
(1)①,由EG⊥BC,EF⊥AB结合∠ABC=∠BFE=∠BGE=90°可得四边形BGEF是矩形,再由∠ABD=45°即可得证;
②,由正方形性质知∠A=90°、∠ABD=45°,据此可得![]() 的值、EF∥AD,利用平行线分线段成比例定理可得;
的值、EF∥AD,利用平行线分线段成比例定理可得;
(2)连接BE,只需证△DBE∽△CBG即可得;
(3),根据相似三角形的判定得到△BCH∽△DGB,由相似三角形的性质得到![]() ,设BG=a,BC=x,带入
,设BG=a,BC=x,带入![]() ,联立Rt△BGD中,勾股定理得BD2=BG2+DG2,计算得到答案.
,联立Rt△BGD中,勾股定理得BD2=BG2+DG2,计算得到答案.
(1)①∵四边形ABCD是正方形,
∴∠ABC=90°,∠ABD=45°.
∵EG⊥BC,EF⊥AB,
∴∠ABC=∠BFE=∠BGE=90°,
∴四边形CEGF是矩形,∠ABD=∠CBD=45°,
∴BF=EF,
∴四边形BGEF是正方形
∴EF∥AD
∴△BEF∽△BDA
②由①知四边形BGEF是正方形,△BEF∽△BDA
∴∠BAD=90°,∠ABD=45°,
∴![]() =
=![]() ,△BEF∽△BDA,
,△BEF∽△BDA,
∴![]() =
=![]() ;
;
(2)
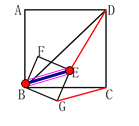
连接BE,
△DBC∽△EBG(两等腰直角三角形相似)
∴![]()
∴![]()
又∵∠DBE=∠CBG
∴△DBE∽△CBG
∴![]()
(3)∵∠DBE=∠CBG,∠DBE+∠BDE=45°∠CBG+∠HBC=45°
∴∠BDG=∠HBC
又∠G=∠BCH=90°
△BCH∽△DGB
设BG=a,BC=x
![]() ,即
,即![]() ,得x2=(a+1)(a+3)①
,得x2=(a+1)(a+3)①
在Rt△BGD中,勾股定理得BD2=BG2+DG2
即2x2=a2+(a+3)2②
联立①②得a=![]() ,x=
,x=![]() ,故BC=
,故BC=![]() .
.