题目内容
【题目】一艘货轮以36km/h的速度在海面上沿正北方向航行，当行驶至A处时，发现北偏东37°方向有一个灯塔B，货轮继续向北航行20分钟后到达C处，发现灯塔B在它的北偏东67°方向，则此时货轮与灯塔B的距离为_____km．（结果精确到0.1，参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，sin67°≈0.920，cos67°≈0.391，tan67°≈2.356）
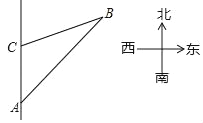
【答案】22.0
【解析】
作BH⊥AC交AC的延长线于H，设BH＝xkm，利用正切的定义用x表示出AH，CH，根据题意列方程求出x，根据正弦的定义计算．
作BH⊥AC交AC的延长线于H，
设BH＝xkm，
在Rt△AHB中，tan∠HAB＝
，
则AH＝
x，
在Rt△CHB中，tan∠HCB＝
，
则CH＝
，
由题意得，
x﹣
＝36×
，
解得，x≈13.20，
在Rt△CHB中，BC＝
≈22.0（km），
故答案为：22.0．
练习册系列答案
相关题目
