Question

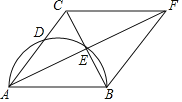
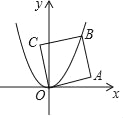
【题目】如图，四边形ABCD和四边形AEFG均为菱形，且∠EAG＝∠ABC．

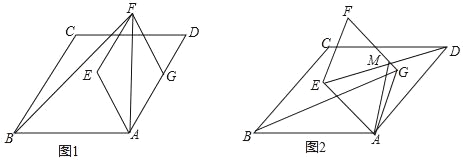
（1）如图1，点G在线段AD上，已知AD＝5，AG＝3，且cos∠ABC＝ ，连接AF，BF，求BF的长；

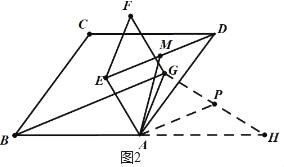
（2）如图2，点G在菱形ABCD内部，连接BG、DE，若点M为DE中点，试猜想AM与BG之间的数量关系，并证明你的结论．

Answer 1

【答案】（1）BF=；（2）BG＝2AM，见解析.

【解析】

（1）由cos∠ABC＝得到∠EAG＝∠ABC＝60°，由AF为菱形对角线得到AF平分∠EAG，求得∠BAF＝90°．已知AB＝AD＝5，所以在Rt△ABF中只要求出AF即能求出BF．又因为AF为菱形对角线且已知菱形边长为3，连接另一对角线EG，根据对角线互相垂直平分且∠FAG＝30°即能求出BF．

（2）图形比较复杂，关键条件为∠EAG＝∠ABC的运用．因为菱形中∠ABC与∠BAD互补，则∠ABC与∠BAD的补角相等，延长BA构造∠DAH＝∠ABC，所以∠EAG＝∠DAH，中间加上公共角∠DAG，易得∠EAD＝∠GAH且EA＝GA，所以使BA的延长线AH＝AD即能构造出△ADE≌△AHG．取GH中点P，则AM、AP为全等三角形对应中线，AM＝AP，问题转化为AP与BG的数量关系．又A、P分别为BH、GH中点，根据中位线定理，BG＝2AP，得证．

解：（1）连接EG，交AF于点O，（如图1）

∵四边形AEFG为菱形

∴EG⊥AF，AF＝2OA，AF平分∠EAG

∵cos∠ABC＝，

∴∠EAG＝∠ABC＝60°

∴∠OAG＝∠EAG＝30°

∵AG＝3，∠AOG＝90°

∴OG＝AG＝

∴OA＝＝

∴AF＝2OA＝

∵菱形ABCD中，∠ABC＝60°，AD∥BC，AB＝5

∴∠BAD＝180°﹣∠ABC＝120°，AD＝AB＝5

∴∠BAF＝∠BAD﹣∠DAF＝120°﹣30°＝90°

∴BF＝

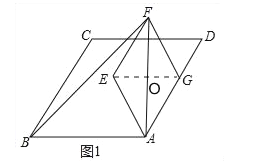
（2）猜想BG＝2AM，证明如下：

延长BA至H，使AH＝AB，连接GH，取GH中点P，连接AP，（如图2）

∵四边形ABCD和四边形AEFG为菱形

∴AD＝AB＝AH，AE＝AG，BC∥AD

∴∠ABC＝∠HAD

∵∠EAG＝∠ABC

∴∠EAG＝∠HAD

∴∠EAG+∠DAG＝∠HAD+∠DAG

即∠EAD＝∠GAH

在△ADE与△AHG中

，

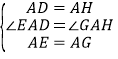∴△ADE≌△AHG（SAS）

∵M是DE中点，P是GH中点，即AM与AP为全等三角形对应中线

∴AM＝AP

∵A为BH中点，

∴AP为△BGH中位线

∴BG＝2AP

∴BG＝2AM