题目内容
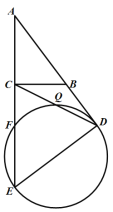
【题目】如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A
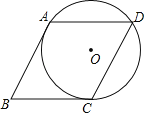
(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
【答案】解:(1)证明:如图,连接OA、OB、OC,
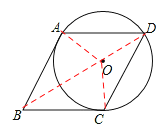
∵AB与⊙O切于A点,∴OA⊥AB,即∠OAB=90°。
∵四边形ABCD为菱形,∴BA=BC。
在△ABO和△CBO中,∵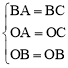 ,
,
∴△ABC≌△CBO(SSS)。∴∠BOC=∠OAC=90°。∴OC⊥BC。
∵OC是⊙O的半径,∴BC为⊙O的切线。
(2)连接BD,
∵△ABC≌△CBO,∴∠AOB=∠COB。
∵四边形ABCD为菱形,∴BD平分∠ABC,CB=CD。
∴点O在BD上。
∵∠BOC=∠ODC+∠OCD,而OD=OC,∴∠ODC=∠OCD。
∴∠BOC=2∠ODC。
∵CB=CD,∴∠OBC=∠ODC。∴∠BOC=2∠OBC。
∵∠BOC+∠OBC=90°,∴∠OBC=30°。∴∠ABC=2∠OBC=60°
【解析】
试题(1)连接OA、OB、OC、BD,根据切线的性质得OA⊥AB,即∠OAB=90°,再根据菱形的性质得BA=BC,然后根据“SSS”可判断△ABC≌△CBO,则∠BOC=∠OAC=90°,于是可根据切线的判定方法即可得到结论。
(2)由△ABC≌△CBO得∠AOB=∠COB,则∠AOB=∠COB,由于菱形的对角线平分对角,所以点O在BD上,利用三角形外角性质有∠BOC=∠ODC+∠OCD,则∠BOC=2∠ODC,由于CB=CD,则∠OBC=∠ODC,所以∠BOC=2∠OBC,根据∠BOC+∠OBC=90°可计算出∠OBC=30°,然后利用∠ABC=2∠OBC计算即可。

练习册系列答案
相关题目