题目内容
【题目】如图,抛物线y=x2+x﹣2与x轴交于A,B两点,与y轴交于点C.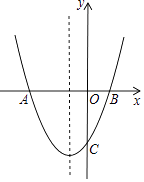
(1)求点A,点B和点C的坐标;
(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;
(3)若点M是直线AC下方抛物线上一动点,求四边形ABCM面积的最大值.
【答案】
(1)
解:由 y=0,得 x2+x﹣2=0 解得 x1=﹣2, x2=1,
∴A(﹣2,0),B(1,0),
由 x=0,得 y=﹣2,
∴C(0,﹣2)
(2)
解:连接AC与对称轴的交点即为点P.
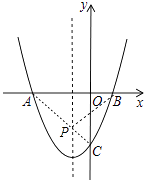
设直线 AC 为 y=kx+b,则﹣2k+b=0,b=﹣2:得 k=﹣1,y=﹣x﹣2.
对称轴为 x=﹣ ![]() ,当 x=﹣
,当 x=﹣ ![]() 时,y=_(﹣
时,y=_(﹣ ![]() )﹣2=﹣
)﹣2=﹣ ![]() ,
,
∴P(﹣ ![]() ,﹣
,﹣ ![]() )
)
(3)
解:过点M作MN丄x轴与点N,
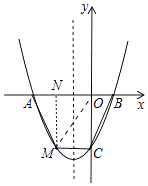
设点M(x,x2+x﹣2),则AN=x+2,0N=﹣x,0B=1,0C=2,MN=﹣(x2+x﹣2)=﹣x2﹣x+2,
S 四边形ABCM=S△AOM+S△OCM+S△BOC= ![]() (x+2)(﹣x2﹣x+2)+
(x+2)(﹣x2﹣x+2)+ ![]() (2﹣x2﹣x+2)(﹣x)+
(2﹣x2﹣x+2)(﹣x)+ ![]() ×1×2
×1×2
=﹣x2﹣2x+3
=﹣(x+1)2+4.
∵﹣1<0,
∴当x=_l时,S四边形ABCM的最大值为4
【解析】(1)利用待定系数法即可解决问题.(2)连接AC与对称轴的交点即为点P.求出直线AC的解析式即可解决问题.(3)过点M作MN丄x轴与点N,设点M(x,x2+x﹣2),则AN=x+2,0N=﹣x,0B=1,0C=2,MN=﹣(x2+x﹣2)=﹣x2﹣x+2,根据S 四边形ABCM=S△AOM+S△OCM+S△BOC构建二次函数,利用二次函数的性质即可解决问题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目