题目内容
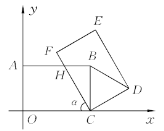
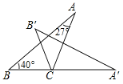
【题目】如图,将![]() 绕点C按顺时针方向旋转至
绕点C按顺时针方向旋转至![]() ,使点
,使点![]() 落在BC的延长线上
落在BC的延长线上![]() 已知∠A=27°,∠B=40° ,则
已知∠A=27°,∠B=40° ,则![]() ___度
___度![]()
【答案】46
【解析】
根据三角形外角的性质求出∠ACA′=67°,再由△ABC绕点C按顺时针方向旋转至△A′B′C,得到△ABC≌△A′B′C,证明∠BCB′=∠ACA′,利用平角即可解答.
解:∵∠A=27°,∠B=40°,
∴∠ACA′=∠A+∠B=27°+40°=67°,
根据旋转的性质知,△ABC≌△A′B′C,
∴∠ACB=∠A′CB′,
∴∠ACB-∠B′CA=∠A′CB-∠B′CA,
即∠BCB′=∠ACA′,
∴∠BCB′=67°,
∴∠ACB′=180°-∠ACA′-∠BCB′=180°-67°-67°=46°,
故答案为:46.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目