题目内容
【题目】如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:△CDF∽△BGF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.
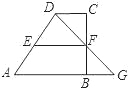
【答案】(1)证明见解析(2)CD=2cm
【解析】
试题分析:(1)利用平行线的性质可证明△CDF∽△BGF.
(2)根据点F是BC的中点这一已知条件,可得△CDF≌△BGF,则CD=BG,只要求出BG的长即可解题.
试题解析:(1)∵梯形ABCD,AB∥CD,
∴∠CDF=∠G,∠DCF=∠GBF,
∴△CDF∽△BGF.
(2)由(1)△CDF∽△BGF,
又∵F是BC的中点,BF=FC,
∴△CDF≌△BGF,
∴DF=GF,CD=BG,
∵AB∥DC∥EF,F为BC中点,
∴E为AD中点,
∴EF是△DAG的中位线,
∴2EF=AG=AB+BG.
∴BG=2EF﹣AB=2×4﹣6=2,
∴CD=BG=2cm.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目