题目内容
【题目】如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的圆O交BC于点D,且D点是弧BE的中点,
(1)求证AB是圆的直径;
(2)若AB=8,∠C=60°,求阴影部分的面积;
(3)当∠A为锐角时,试说明∠A与∠CBE的关系.
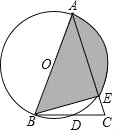
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)连接AD,根据等腰三角形的三线合一得到AD⊥BC,根据圆周角定理的推论证明;
(2)连接OE,根据扇形面积公式计算即可.
(3)AB是直径,根据直径所对的圆周角是直角得到∠BEA=90°,∠EBC+∠C=∠CAD+∠C=90° ,根据同角的余角相等得到∠EBC=∠CAD,即可得到∠A与∠CBE的关系.
(1)连结AD,
∵D是弧BE中点,
∴∠BAD=∠CAD-
又∵AB=AC,
∴AD⊥BD
∴∠ADB=90°,
∴AB是直径.
(2)连结OE,S扇形AOE=![]() ,
,
S△BOE=![]() ,
,
S阴影=![]() +
+![]()
(3)由(1)AB是直径,
∴∠BEA=90°
∴∠EBC+∠C=∠CAD+∠C=90° ,
∴∠EBC=∠CAD
∴∠CAB=2∠EBC

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目