题目内容
14. 如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N
如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N(1)求证:AE=MN;
(2)若AE=2,∠DAE=30°,求正方形的边长.
分析 (1)连接EC,根据题意可得出四边形EMCN为矩形,故MN=CE,再由SAS定理得出△ABE≌△CBE,进而可得出结论;
(2)过点E作EF⊥AD,由直角三角形的性质可得出EF及AF的长,再由等腰直角三角形的性质得出DF的长,进而可得出结论.
解答 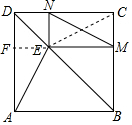 (1)证明:连接EC.
(1)证明:连接EC.
∵四边形ABCD是正方形,EM⊥BC,EN⊥CD,
∴∠NCM=∠CME=∠CNE=90°,
∴四边形EMCN为矩形.
∴MN=CE.
又∵BD为正方形ABCD的对角线,
∴∠ABE=∠CBE.
在△ABE和△CBE中
∵$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBE}\\{BE=BE}\end{array}\right.$,
∴△ABE≌△CBE(SAS).
∴AE=EC.
∴AE=MN.
(2)解:过点E作EF⊥AD于点F,
∵AE=2,∠DAE=30°,
∴EF=$\frac{1}{2}$AE=1,AF=AE•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∵BD是正方形ABCD的对角线,
∴∠EDF=45°,
∴DF=EF=1,
∴AD=AF+DF=$\sqrt{3}$+1,即正方形的边长为$\sqrt{3}$+1.
点评 本题考查的是正方形的性质,熟知正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角是解答此题的关键.

练习册系列答案
相关题目
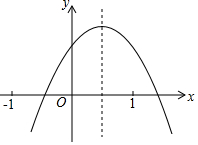 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论 ①a+b+c<0②a-b+c<0③b+2a<0④abc>0(5)b2<4ac,其中正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论 ①a+b+c<0②a-b+c<0③b+2a<0④abc>0(5)b2<4ac,其中正确的个数是( ) 如图,直线l1过点A(0,2),点B(2,0),直线l2:y=$\frac{1}{2}$x+1与y轴交于点D,与x轴交于点E,两直线l1、l2相交于点C.
如图,直线l1过点A(0,2),点B(2,0),直线l2:y=$\frac{1}{2}$x+1与y轴交于点D,与x轴交于点E,两直线l1、l2相交于点C.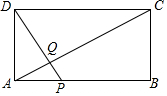 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q. 如图,∠AOB=60°,点P在∠AOB的内部,且点P到OA、OB的距离为a和b,且a<b,点M在OA上,点N在OB上,则PM+MN的最小值为a+b.
如图,∠AOB=60°,点P在∠AOB的内部,且点P到OA、OB的距离为a和b,且a<b,点M在OA上,点N在OB上,则PM+MN的最小值为a+b.