Question

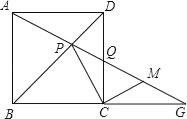
【题目】如图，在正方形ABCD中，P是BD上一点，AP的延长线交CD于点Q，交BC的延长线于点G，点M是GQ的中点，连接CM．求证：PC⊥MC．

Answer 1

【答案】见解析

【解析】分析：根据正方形的性质可得出∠ADP=∠CDP、AD=CD，结合DP=DP即可证出△ADP≌△CDP（SAS），根据全等三角形的性质可得出∠DCP=∠DAG，由AD∥BG可得出∠DAG=∠G，进而得出∠DCP=∠G，由直角三角形斜边上中线等于斜边的一半可得出∠MCQ=∠MQC，再结合∠G、∠MQC互余，即可证出∠DCP+∠MCQ=90°，即PC⊥MC．

详解：证明：∵BD为正方形ABCD的对角线，

∴∠ADP=∠CDP，AD=CD．

在△ADP和△CDP中，

，

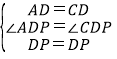∴△ADP≌△CDP（SAS），

∴∠DCP=∠DAG．

又∵四边形ABCD为正方形，

∴AD∥BG，

∴∠DAG=∠G．

∴∠DCP=∠G．

又∵∠QCG=90°，M为GQ中点，

∴CM=QM，

∴∠MCQ=∠MQC．

又∵∠G+∠MQC=90°，

∴∠DCP+∠MCQ=90°，

∴PC⊥MC．