题目内容
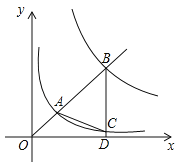
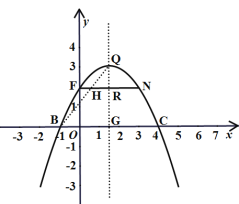
【题目】如图,在平面直角坐标系![]() 中,已知二次函数图象与
中,已知二次函数图象与![]() 正半轴交于点
正半轴交于点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() .若过点
.若过点![]() 作平行于
作平行于![]() 轴的直线交抛物线于点
轴的直线交抛物线于点![]() .
.
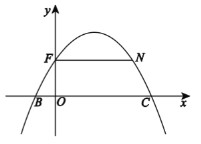
(1)点![]() 的横坐标为______;
的横坐标为______;
(2)设抛物线的顶点为点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,该二次函数有最大值3,试求
时,该二次函数有最大值3,试求![]() 的值.
的值.
【答案】(1)3;(2)![]() ;(3)
;(3)![]() 3或2.
3或2.
【解析】
(1)根据抛物线的对称性求解即可;
(2)先利用待定系数法确定二次函数的解析式,表示出顶点坐标,过![]() 作
作![]() 于
于![]() ,用特殊角的三角函数值得到关于m的不等式,解不等式即可;
,用特殊角的三角函数值得到关于m的不等式,解不等式即可;
(3)分当![]() 时、
时、![]() 时两种情况,利用函数的增减性求解即可.
时两种情况,利用函数的增减性求解即可.
(1)∵抛物线与![]() 轴分别交于点
轴分别交于点![]()
∴对称轴为![]()
∴N点的横坐标为3;
故答案为:3
(2)设抛物线解析式为![]()
抛物线经过![]()
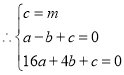 解得
解得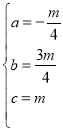
![]()
![]() 顶点
顶点![]()
过![]() 作
作![]() 于
于![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
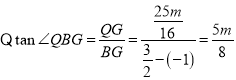
![]()
![]()
(3)![]()
![]() 对称轴为
对称轴为![]()
∵m>0,
∴m+2>![]() ,故不存在m+2<
,故不存在m+2<![]() 这种情况.
这种情况.
①当![]() <m+2时,
<m+2时,![]() 时
时![]() 有最大值,
有最大值,
![]()
解得![]() ,舍去
,舍去
②当![]() 时,开口向下,当
时,开口向下,当![]() 时,
时,![]() 随着
随着![]() 的增大而减小,
的增大而减小,
![]() 时
时![]() 有最大值.
有最大值.
![]()
![]()
![]()
![]() (舍去)
(舍去)
综上所述,![]() 3或2.
3或2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目