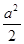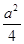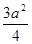题目内容
如图,点D、E在△ABC的边BC上,AB=AC,AD=AE,且BD=4,求EC的长.
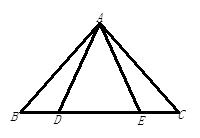
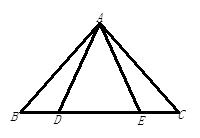
4
试题分析:直观上看BD=CE,证明线段相等的方法一般是全等,包含BD和CE的两个三角形是△ABD和△AEC,找两个三角形全等的条件,因为AB=AC,所以∠B=∠C,又因为AD=AE,所以∠ADE=∠AED,即∠ADB=∠AEC,在△ABD和△AEC中,∠B=∠C,∠ADB=∠AEC,AB=AC,所以△ABD≌△AEC(AAS),所以EC=BD=4.
试题解析:∵AB=AC,
∴∠B=∠C,
又∵AD=AE,
∴∠ADE=∠AED,即∠ADB=∠AEC,
在△ABD和△AEC中, ∠B=∠C, ∠ADB=∠AEC, AB=AC,
∴△ABD≌△AEC(AAS),
∴EC=BD=4.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
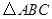 中,
中,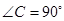 ,
,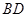 平分
平分 交AC于点D,若CD=6,则点D到AB的距离为 .
交AC于点D,若CD=6,则点D到AB的距离为 .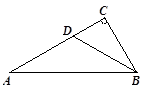

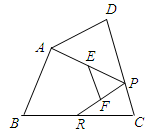
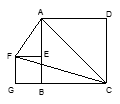
 ,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )
,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )