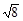题目内容
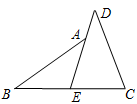
如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC= °.
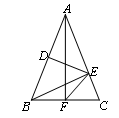

45.
试题分析:∵DE垂直平分AB,∴AE=BE.
∵BE⊥AC,∴△ABE是等腰直角三角形. ∴∠BAC=∠ABE=45°.
又∵AB=AC,∴∠ABC=
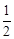 (180°-∠BAC)=(180°-45°)=67.5°.
(180°-∠BAC)=(180°-45°)=67.5°.∴∠CBE=∠ABC-∠ABE=67.5°-45°=22.5°.
∵AB=AC,AF⊥BC,∴BF="CF." ∴BF=EF.
∴∠BEF=∠CBE=22.5°,∴∠EFC=∠BEF+∠CBE=22.5°+22.5°=45°.

练习册系列答案
相关题目
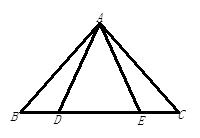
 B.
B. 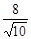 C.
C.  D.
D.