题目内容
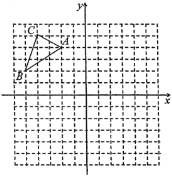
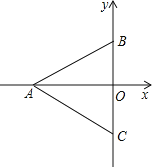
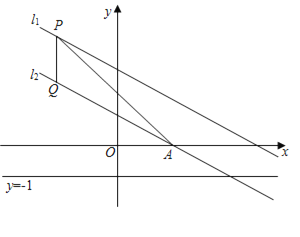
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x+2向下平移1个单位后,得到直线l2,l2交x轴于点A,点P是直线l1上一动点,过点P作PQ∥y轴交l2于点Q
x+2向下平移1个单位后,得到直线l2,l2交x轴于点A,点P是直线l1上一动点,过点P作PQ∥y轴交l2于点Q
(1)求出点A的坐标;
(2)连接AP,当△APQ为以PQ为底边的等腰三角形时,求点P和点Q的坐标;
(3)点B为OA的中点,连接OQ、BQ,若点P在y轴的左侧,M为直线y=﹣1上一动点,当△PQM与△BOQ全等时,求点M的坐标.
【答案】(1)A(2,0);(2)P(3,![]() ),Q(3,﹣
),Q(3,﹣![]() );(3)M(﹣1,﹣1)或(﹣1,8)
);(3)M(﹣1,﹣1)或(﹣1,8)
【解析】
(1)求出直线l2的解析式为y=﹣![]() x+1,即可求A的坐标;
x+1,即可求A的坐标;
(2)设点P(x,﹣![]() x+2),Q(x,﹣
x+2),Q(x,﹣![]() x+1),由AQ=AP,即可求P点坐标;
x+1),由AQ=AP,即可求P点坐标;
(3)设P(n,﹣![]() n+2),M(m,﹣1),则Q(n,﹣
n+2),M(m,﹣1),则Q(n,﹣![]() n+1),可求出BQ=
n+1),可求出BQ=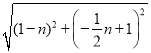 ,OQ=
,OQ=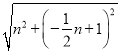 ,PM=
,PM=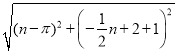 ,QM=
,QM=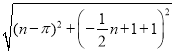 ,①当△PQM≌△BOQ时,PM=BQ,QM=OQ,结合勾股定理,求出m;②当△QPM≌△BOQ时,有PM=OQ,QM=BQ,结合勾股定理,求出m即可.
,①当△PQM≌△BOQ时,PM=BQ,QM=OQ,结合勾股定理,求出m;②当△QPM≌△BOQ时,有PM=OQ,QM=BQ,结合勾股定理,求出m即可.
解:(1)∵直线l1:y=﹣![]() x+2向下平移1个单位后,得到直线l2,
x+2向下平移1个单位后,得到直线l2,
∴直线l2的解析式为y=﹣![]() x+1,
x+1,
∵l2交x轴于点A,
∴A(2,0);
(2)当△APQ为以PQ为底边的等腰三角形时,
∴AQ=AP,
∵点P是直线l1上一动点,
设点P(x,﹣![]() x+2),
x+2),
∵过点P作PQ∥y轴交l2于点Q
∴Q(x,﹣![]() x+1),
x+1),
∴(﹣![]() x+2)2=(﹣
x+2)2=(﹣![]() x+1)2,
x+1)2,
∴x=3,
∴P(3,![]() ),Q(3,﹣
),Q(3,﹣![]() );
);
(3)∵点B为OA的中点,
∴B(1,0),
∴PQ=BO=1,
设P(n,﹣![]() n+2),M(m,﹣1),则Q(n,﹣
n+2),M(m,﹣1),则Q(n,﹣![]() n+1),
n+1),
∴BQ=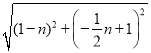 ,OQ=
,OQ=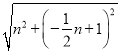 ,
,
PM=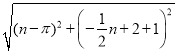 ,QM=
,QM=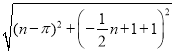 ,①
,①
∵△PQM与△BOQ全等,
①当△PQM≌△BOQ时,
有PM=BQ,QM=OQ,
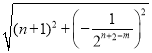 =
=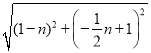 ,
,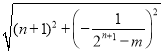 =
=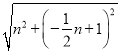 ,
,
∴n=2m﹣2,
∵点P在y轴的左侧,
∴n<0,
∴m<1,
∴m=﹣1,
∴M(﹣1,﹣1);
②当△QPM≌△BOQ时,
有PM=OQ,QM=BQ,
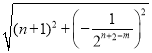 =
=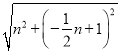 ,
,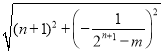 =
=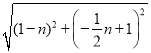 ,
,
∴n=![]() ﹣
﹣![]() m,
m,
∵点P在y轴的左侧,
∴n<0,
∴m>2,
∴m=8,
∴M(﹣1,8);
综上所述,M(﹣1,﹣1)或M(﹣1,8).1:y=﹣![]() x+2向下平移1个单位后,得到直线l2,
x+2向下平移1个单位后,得到直线l2,

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案