题目内容
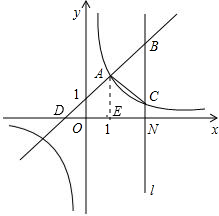
如图,一次函数y=kx+1(k≠0)与反比例函数y= (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.

(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
 (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
(1)y=x+1 y=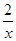 (2)
(2)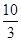
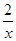 (2)
(2)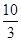
(1)将A坐标代入一次函数解析式中求出k的值,确定出一次函数解析式,将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例解析式;
(2)设一次函数与x轴交点为D点,过A作AE垂直于x轴于E,三角形ABC面积=三角形BDN面积-三角形ADE面积-梯形AECN面积,求出即可.
(1)将A(1,2)代入一次函数解析式得:k+1=2,即k=1,
∴一次函数解析式为y=x+1;
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为y=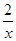 ;
;
(2)设一次函数与x轴交于D点,过A作AE垂直于x轴于E,令y=0,求出x=-1,即OD=1,
∵A(1,2),
∴AE=2,OE=1,
∵直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
∴点B、C的横坐标为3,
将x=3代入一次函数得:y=4,将x=3代入反比例解析式得:y=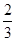 ,
,
∴B(3,4),即ON=3,BN=4,C(3,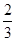 ),即CN=
),即CN=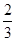 ,
,
则S△ABC=S△BDN-S△ADE-S梯形AECN=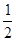 ×4×4-
×4×4-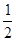 ×2×2-
×2×2-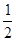 ×(
×(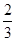 +2)×2=
+2)×2=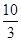 .
.
(2)设一次函数与x轴交点为D点,过A作AE垂直于x轴于E,三角形ABC面积=三角形BDN面积-三角形ADE面积-梯形AECN面积,求出即可.
(1)将A(1,2)代入一次函数解析式得:k+1=2,即k=1,
∴一次函数解析式为y=x+1;
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为y=
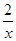 ;
;
(2)设一次函数与x轴交于D点,过A作AE垂直于x轴于E,令y=0,求出x=-1,即OD=1,
∵A(1,2),
∴AE=2,OE=1,
∵直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
∴点B、C的横坐标为3,
将x=3代入一次函数得:y=4,将x=3代入反比例解析式得:y=
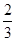 ,
,∴B(3,4),即ON=3,BN=4,C(3,
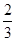 ),即CN=
),即CN=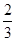 ,
,则S△ABC=S△BDN-S△ADE-S梯形AECN=
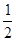 ×4×4-
×4×4-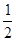 ×2×2-
×2×2-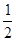 ×(
×(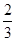 +2)×2=
+2)×2=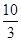 .
.
练习册系列答案
相关题目
 与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:

 与
与 轴相交于点A,与
轴相交于点A,与 轴相交于点B.
轴相交于点B.
 ,试求点P的坐标.
,试求点P的坐标. 时,函数
时,函数 与
与 在同一坐标系中的图象大致是( )
在同一坐标系中的图象大致是( )

 ,则a的值是( )
,则a的值是( )


