题目内容
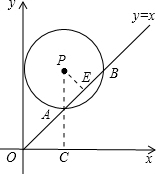
如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
,则a的值是( )

 ,则a的值是( )
,则a的值是( )
A. | B. | C. | D. |
A.
试题分析:过P点作PE⊥AB于E,连接PA并延长PA交x轴于点C.
∵PE⊥AB,AB=2∴AE=
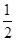 AB=1,
AB=1,∵PA=
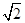 ,
,在Rt△PAE中,由勾股定理得:PE=1,
∴PE=AE,∴∠PAE=45°,
∵函数y=x的图象与y轴的夹角为45°,
∴y轴∥PA,∴∠PCO=90°,
∴A点的横坐标为
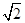 ,
,∵A点在直线y=x上,
∴A点的纵坐标为
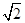 ,
,∴PC=2
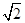 ,
,∴a=2
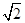 .
.故选A.
考点: 1.切线的判定;2.一次函数图象上点的坐标特征;3.勾股定理;4.垂径定理.

练习册系列答案
相关题目
 (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
 的图象没有公共点,则( )
的图象没有公共点,则( ) ,
, 相交于点
相交于点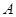 ,
, 轴的交点坐标为
轴的交点坐标为 ,
, 轴的交点坐标为
轴的交点坐标为 ,结合图象解答下列问题:(每小题4分,共8分)
,结合图象解答下列问题:(每小题4分,共8分) .
.
 在同一坐标系数中的大致图象是( )
在同一坐标系数中的大致图象是( )





 或
或 .
.