题目内容
【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
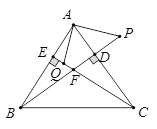
求证:(1)AP=AQ ;
(2)AP⊥AQ.
【答案】详见解析
【解析】
(1)由于BD⊥AC,CE⊥AB,可得∠ABD=∠ACE,又有对应边的关系,进而得出△ABP≌△QCA;
(2)在(1)的基础上,证明∠PAQ=90°即可.
解:(1)∵BD⊥AC,CE⊥AB(已知),
∴∠BEC=∠BDC=90°,∠ABD+∠BAC=90°,∠ACE+∠BAC=90°
∴∠ABD=∠ACE
在△ABP和△QCA中
∵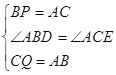
∴△ABP≌△QCA(SAS)
∴AP=AQ
(2)由(1)可得∠CAQ=∠P
∵BD⊥AC(已知),即∠P+∠CAP=90°
∴∠CAQ+∠CAP=90°,
即∠QAP=90°,
∴AP⊥AQ
考点: 全等三角形的判定与性质.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 (单位:亩) | 种植B类蔬菜面积 (单位:亩) | 总收入 (单位:元) |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.


