Question

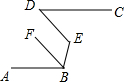
如图（a），木杆EB与FC平行，木杆的两端B、C用一橡皮筋连接．

（1）在图（a）中，∠B与∠C有何关系？
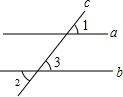
（2）若将橡皮筋拉成图（b）的形状，则∠A，∠B，∠C之间有何关系？
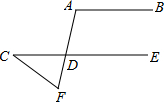
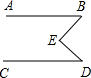
（3）若将橡皮筋拉成图（c）的形状，则∠A，∠B，∠C之间有何关系？
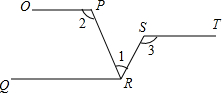
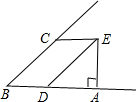
（4）若将橡皮筋拉成图（d）的形状，则∠A，∠B，∠C之间有何关系？
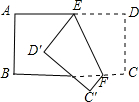
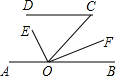
（5）若将橡皮筋拉成图（e）的形状，则∠A，∠B，∠C之间有何关系？

Answer 1

（1）∵EB∥FC，
∴∠B+∠C=180°；

（2）如图，过点A作AD∥EB，
则∠BAD=∠B，∠CAD=∠C，
∴∠BAD+∠CAD=∠B+∠C，
即∠A=∠B+∠C；

（3）如图，过点A作AD∥EB，
则∠B+∠BAD=180°，∠C+∠CAD=180°，
∴∠B+∠BAD=∠C+∠CAD=180°+180°，
即∠A+∠B+∠C=360°；

（4）由三角形的外角性质，∠1=∠A+∠B，
∵EB∥FC，
∴∠1=∠C，
∴∠A+∠B=∠C；

（5）由三角形的外角性质，∠1=∠A+∠C，
∵EB∥FC，
∴∠1=∠B，
∴∠A+∠C=∠B．