ĢāÄæÄŚČŻ
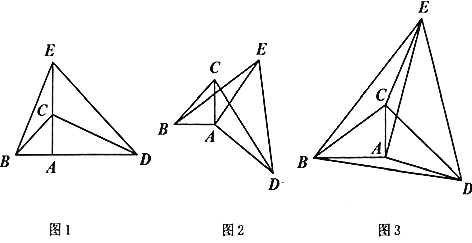
”¾ĢāÄæ”æ£Ø1£©ŌŚŅ»½ŚŹżŃ§Ģ½¾ææĪÉĻ£¬Ń§ÉśĆĒ·¢ĻÖĮĖŅ»øö¹ęĀÉ£ŗ
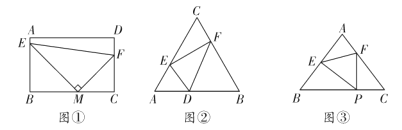
ČēĶ¼¢Ł£¬µ±ĖıߊĪ![]() ŹĒ¾ŲŠĪŹ±£¬
ŹĒ¾ŲŠĪŹ±£¬![]() µÄÖ±½Ē¶„µćMŌŚ
µÄÖ±½Ē¶„µćMŌŚ![]() ±ßÉĻŌĖ¶Æ£¬Ö±½Ē±ß·Ö±šÓėĻ߶Ī
±ßÉĻŌĖ¶Æ£¬Ö±½Ē±ß·Ö±šÓėĻ߶Ī![]() ”¢Ļ߶Ī
”¢Ļ߶Ī![]() ½»ÓŚE”¢FĮ½µć£¬ŌŚµćMŌĖ¶ÆµÄ¹ż³ĢÖŠ£¬Ź¼ÖÕ“ęŌŚ×Å
½»ÓŚE”¢FĮ½µć£¬ŌŚµćMŌĖ¶ÆµÄ¹ż³ĢÖŠ£¬Ź¼ÖÕ“ęŌŚ×Å![]() .ÓŚŹĒÓÖÓŠĶ¬Ń§Ģį³öĮĖĪŹĢā£¬Čē¹ū½«ĖıߊĪ»»³ÉČż½ĒŠĪŹ±£¬ŹĒ·ńČŌ“ęŌŚĶ¬ŃłµÄ¹ęĀÉÄŲ£æČēĶ¼¢Ś£¬ŌŚ
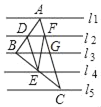
.ÓŚŹĒÓÖÓŠĶ¬Ń§Ģį³öĮĖĪŹĢā£¬Čē¹ū½«ĖıߊĪ»»³ÉČż½ĒŠĪŹ±£¬ŹĒ·ńČŌ“ęŌŚĶ¬ŃłµÄ¹ęĀÉÄŲ£æČēĶ¼¢Ś£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬µćDĪŖ
£¬µćDĪŖ![]() ±ßÉĻµÄ¶Æµć£¬¹żµćD×÷
±ßÉĻµÄ¶Æµć£¬¹żµćD×÷![]() £¬½»
£¬½»![]() ÓŚµćE£¬½»
ÓŚµćE£¬½»![]() ÓŚµćF£¬ĒėĪŹŹĒ·ń“ęŌŚĮ½øöĻąĖʵÄČż½ĒŠĪ£¬Čō“ęŌŚ£¬ĒėÖ¤Ć÷£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
ÓŚµćF£¬ĒėĪŹŹĒ·ń“ęŌŚĮ½øöĻąĖʵÄČż½ĒŠĪ£¬Čō“ęŌŚ£¬ĒėÖ¤Ć÷£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø2£©½įŗĻÉĻŹö¹ęĀÉ£¬½ā¾öĻĀĮŠĪŹĢā£ŗ
ČēĶ¼¢Ū£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬µćPĪŖ
£¬µćPĪŖ![]() ÉĻŅ»µć£Ø²»ÓėB”¢CÖŲŗĻ£©£¬¹żµćP×÷
ÉĻŅ»µć£Ø²»ÓėB”¢CÖŲŗĻ£©£¬¹żµćP×÷![]() ÓŚµćE£¬
ÓŚµćE£¬![]() ½»
½»![]() ÓŚµćF£¬Čō
ÓŚµćF£¬Čō![]() ĪŖµČŃüČż½ĒŠĪ£¬Ēó
ĪŖµČŃüČż½ĒŠĪ£¬Ēó![]() µÄ³¤.
µÄ³¤.
”¾“š°ø”æ£Ø1£©“ęŌŚĮ½øöĻąĖʵÄČż½ĒŠĪ£¬![]() £¬Ö¤Ć÷Ļź¼ū½āĪö£»£Ø2£©
£¬Ö¤Ć÷Ļź¼ū½āĪö£»£Ø2£©![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() »ņ
»ņ![]() »ņ2.
»ņ2.
”¾½āĪö”æ
£Ø1£©ÓÉ![]() £¬
£¬![]() £¬
£¬![]() £¬µĆ
£¬µĆ![]() £¬“Ó¶ųÖ¤Ć÷
£¬“Ó¶ųÖ¤Ć÷![]() Óė
Óė![]() ĻąĖĘ£»
ĻąĖĘ£»
£Ø2£©ĻČÖ¤![]() £¬µ±
£¬µ±![]() ĪŖµČŃüČż½ĒŠĪŹ±£¬·Ö
ĪŖµČŃüČż½ĒŠĪŹ±£¬·Ö![]() ŗĶ
ŗĶ![]() ČżÖÖĒéæöĢÖĀŪ£¬·Ö±šĒóµĆ
ČżÖÖĒéæöĢÖĀŪ£¬·Ö±šĒóµĆ![]() µÄ³¤£¬¼“æÉ.
µÄ³¤£¬¼“æÉ.
£Ø1£©“ęŌŚĮ½øöĻąĖʵÄČż½ĒŠĪ£¬![]() £¬ĄķÓÉČēĻĀ£ŗ
£¬ĄķÓÉČēĻĀ£ŗ
ŌŚ![]() ŗĶ
ŗĶ![]() ÖŠ£¬
ÖŠ£¬
”ß![]() £¬
£¬
![]() £¬
£¬
”ą![]() .
.
ÓÖ”ß![]() £¬
£¬
”ą![]() .
.
”ą![]() £»
£»
£Ø2£©”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]()
ÓÖ”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() .
.
”ß![]() ĪŖµČŃüČż½ĒŠĪ£¬Éč
ĪŖµČŃüČż½ĒŠĪ£¬Éč![]() £¬æÉ·ÖŅŌĻĀČżÖÖĒéæöĢÖĀŪ£ŗ
£¬æÉ·ÖŅŌĻĀČżÖÖĒéæöĢÖĀŪ£ŗ
¢Łµ±![]() Ź±£¬Ōņ
Ź±£¬Ōņ![]() £¬
£¬
”ą![]() £¬ČēĶ¼¢Ł£¬¹żµćA×÷
£¬ČēĶ¼¢Ł£¬¹żµćA×÷![]() ½»
½»![]() ÓŚµćG£¬
ÓŚµćG£¬
”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £»
£»
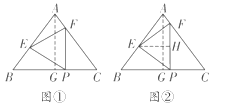
¢Śµ±![]() Ź±£¬ČēĶ¼¢Ś£¬¹żµćA×÷
Ź±£¬ČēĶ¼¢Ś£¬¹żµćA×÷![]() ÓŚµćG£¬¹żµćE×÷
ÓŚµćG£¬¹żµćE×÷![]() ½»
½»![]() ÓŚµćH£¬Ōņ
ÓŚµćH£¬Ōņ![]() .
.
”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬
£¬![]() .
.
”ą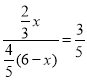 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £»
£»
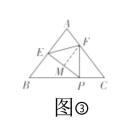
¢Ūµ±![]() Ź±£¬ČēĶ¼¢Ū£¬¹żµćF×÷
Ź±£¬ČēĶ¼¢Ū£¬¹żµćF×÷![]() ½»
½»![]() ÓŚµćM£¬
ÓŚµćM£¬
![]() £¬
£¬
![]() £¬
£¬
”ą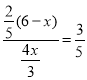 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() .
.
×ŪÉĻĖłŹö£¬![]() µÄ³¤ĪŖ
µÄ³¤ĪŖ![]() »ņ
»ņ![]() »ņ2.
»ņ2.

 »īĮ¦æĪŹ±Ķ¬²½Į·Ļ°²įĻµĮŠ“š°ø
»īĮ¦æĪŹ±Ķ¬²½Į·Ļ°²įĻµĮŠ“š°ø