题目内容
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,已知AD=10,CD=4,B′D=2.
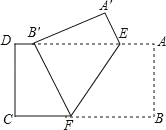
(1)求证:B′E=BF;
(2)求AE的长.
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)首先根据题意得B′F=BF,∠B′FE=∠BFE,接着根据平行线的性质和等腰三角形的判定即可证明B′E=BF;
(2)根据折叠的性质可得AE=A′E,AB=A′B′,在Rt△A′B′E中,根据勾股定理即可得到AE的长.
试题解析:(1)由题意得B′F=BF,∠B′FE=∠BFE,
在矩形ABCD中,AD∥BC,
∴∠B′EF=∠BFE,
∴∠B′FE=∠B′EF,
∴B′F=B′E,
∴B′E=BF;
(2)由折叠的性质可得AE=A′E,AB=A′B′=4,
在Rt△A′B′E中,A′B′2+A′E2=B′E2,
42+A′E2=(10-2-A′E)2,
解得A′E=3,
即AE的长为3.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
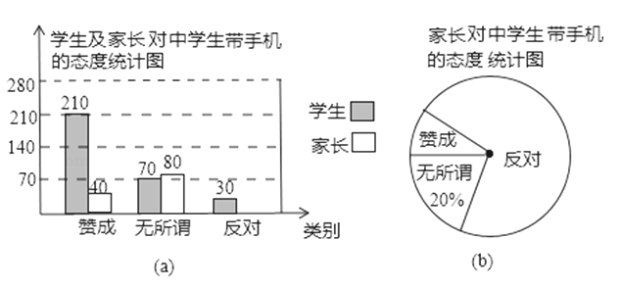
名题训练系列答案【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
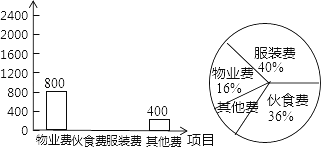
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | ________ | ________ | 400 |
(4)请将条形统计图补充完整.
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?