Question

【题目】已知：在Rt△ABC中，AB⊥BC，点O是AC的中点，连接OB，过C点作CD⊥OB，交BO的延长线于垂足D，BC＝8，sinα＝．

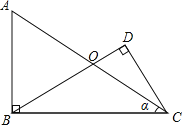
求：（1）线段OC的长；

（2）cos∠DOC的值．

Answer 1

【答案】（1）5；（2）

【解析】

(1)由sinα＝＝，设AB=3x，则AC=5x，由勾股定理得出方程（3x）2+82＝（5x）2，解方程得出AC=10，即可求出OC＝AC＝×10＝5；
(2)由直角三角形斜边上的中线性质得出OB＝OC＝OA＝AC＝5，设OD=y，则BD=OB+OD=5+y，由勾股定理得出方程82﹣（5+y）2＝52﹣y2，得出y=，由三角函数定义即可得出答案．

（1）∵在Rt△ABC中，AB⊥BC，

∴sinα＝＝，

设AB＝3x，则AC＝5x，

∵AB2+BC2＝AC2，

即（3x）2+82＝（5x）2，

解得：x1＝2，x2＝﹣2（不合题意舍去），

∴AC＝10，

∵点O是AC的中点，

∴OC＝AC＝×10＝5；

（2）∵在Rt△ABC中，AB⊥BC，点O是AC的中点，

∴OB＝OC＝OA＝AC＝5，

设OD＝y，则BD＝OB+OD＝5+y，

∵CD⊥OB，

∴CD2＝BC2﹣BD2＝OC2﹣OD2，

∴82﹣（5+y）2＝52﹣y2，

解得：y＝，

∴cos∠DOC＝＝＝．