题目内容
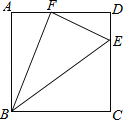
【题目】如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.若sin∠DFE=![]() ,则tan∠EBC的值为( )
,则tan∠EBC的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
首先证得△ABF∽△DFE,sin∠DFE=![]() =
=![]() ,设DE=a,EF=3a,DF=
,设DE=a,EF=3a,DF=![]() =2
=2![]() a,可得出CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,由△ABF∽△DFE,可得tan∠EBC=tan∠EBF=
a,可得出CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,由△ABF∽△DFE,可得tan∠EBC=tan∠EBF=![]() .
.
解:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∵△BCE沿BE折叠为△BFE,
∴∠BFE=∠C=90°,
∴∠AFB+∠DFE=180°﹣∠BFE=90°,
又∵∠AFB+∠ABF=90°,
∴∠ABF=∠DFE,
∴△ABF∽△DFE,
在Rt△DEF中,sin∠DFE=![]() =
=![]() ,
,
∴设DE=a,EF=3a,DF=![]() =2
=2![]() a,
a,
∵△BCE沿BE折叠为△BFE,
∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,
∵△ABF∽△DFE,
∴![]() =
=![]() ,
,
∴tan∠EBF=![]() =
=![]() ,
,
tan∠EBC=tan∠EBF=![]() .
.
故选:A.

练习册系列答案
相关题目