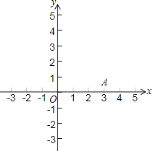题目内容
【题目】现有A、B两个不透明袋子，分别装有3个除颜色外完全相同的小球。其中，A袋装有2个白球，1个红球；B袋装有2个红球，1个白球。
（1）将A袋摇匀，然后从A袋中随机取出一个小球，求摸出小球是白色的概率；
（2）小华和小林商定了一个游戏规则：从摇匀后的A，B两袋中随机摸出一个小球，摸出的这两个小球，若颜色相同，则小林获胜；若颜色不同，则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
【答案】(1)P(摸出白球)＝
；(2)这个游戏规则对双方不公平.
【解析】
(1)根据A袋中共有3个球 ，其中2个是白球，直接利用概率公式求解即可；
(2)列表得到所有等可能的结果，然后分别求出小林获胜和小华获胜的概率进行比较即可.
(1)A袋中共有3个球，其中有2个白球，
∴P(摸出白球)＝；
(2)根据题意，列表如下：
红1 | 红2 | 白 | |
白1 | (白1，红1) | (白1，红2) | (白1，白) |
白2 | (白2，红1) | (白2，红2) | (白2，白) |
红 | (红，红1) | (红，红2) | (红，白) |
由上表可知，共有9种等可能结果，其中颜色相同的结果有4种，颜色不同的结果有5种，
∴P(颜色相同)＝
，P(颜色不同)＝
，
∵＜，
∴这个游戏规则对双方不公平.
【题目】为了解某区八年级学生的睡眠情况，随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人，利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表（单位：小时）
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
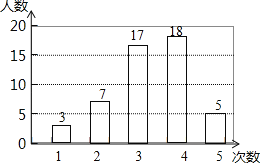
二、学生睡眠情况统计图
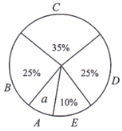
根据图表提供的信息，回答下列问题：
（1）试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数；
（2）如果睡眠时间x（时）满足：
，称睡眠时间合格.已知该区八年级学生有3250人，试估计该区八年级学生睡眠时间合格的共有多少人？
（3）如果将各组别学生睡眠情况分组的最小值（如C组别中，取
），B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
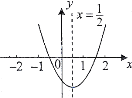
【题目】参照学习函数的过程与方法，探究函数
的图象与性质．因为
，即
，所以我们对比函数
来探究．
列表：
| … | -4 | -3 | -2 | -1 |
|
|
| 2 | 3 | 4 | … |
| … |
|
| 1 | 2 | 4 | -4 | -1 |
| … | ||
| … |
|
| 2 | 3 | 5 | -3 | -1 | 0 |
|
| … |
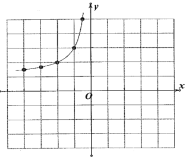
描点：在平面直角坐标系中，以自变量
的取值为横坐标，以
相应的函数值为纵坐标，描出相应的点，如图所示：
（1）①请补全表格，计算
__________．
②请补全图形，用一条光滑曲线顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当
时，
随的增大而__________；（填“增大”或“减小”）
②的图象是由的图象向__________平移__________
③图象关于点__________中心对称．（填点的坐标）
（3）结合函数图象，当
时，求的取值范围．
