题目内容
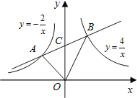
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() (k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
(k≠0)与直线y=ax+b(a≠0)交于A,B两点,直线AB分别交x轴,y轴于C、D两点,若OA=OC,A点坐标为(4,3).
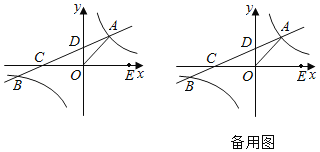
(1)分别求出双曲线与直线的函数表达式;
(2)若P为双曲线上一点,且横坐标为2,H为直线AB上一点,且PH+![]() HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
HC最小,延长PH交x轴于点E,将线段OE沿x轴平移得线段O'E',在平移过程中,是否存在某个位置使|BO'﹣AE'|的值最大值,求出最大值并求出此时E点坐标.
(3)在(2)的情况下,将直线OA沿线段CE平移,平移过程中交y=![]() (x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
(x>0)的图象于M(M与点A不重合)交x轴于点N,在平面内找一点G,使M、N,E,G为顶点的四边形为矩形?直接写出G的坐标.
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ,点E(2,0);(3)G(﹣6,6)
,点E(2,0);(3)G(﹣6,6)
【解析】
(1)由OA=OC,A点坐标为(4,3)可求出C点的坐标,再双曲线与直线的函数表达式即可;
(2)作PK⊥x轴于K,交AC于H,得到![]() =
=![]() ,求得HK=
,求得HK=![]() CH,可得E(2,0),再作B关于x轴的对称点B',B'N∥OE,B'N=OE,连接AN交x轴于E',截取E'O'=OE,则B'N∥E'O',B'N=E'O',得到|BO'﹣AE'|=|E'N'﹣AE'|=AE'﹣E'N=AN,再求最大值即可;
CH,可得E(2,0),再作B关于x轴的对称点B',B'N∥OE,B'N=OE,连接AN交x轴于E',截取E'O'=OE,则B'N∥E'O',B'N=E'O',得到|BO'﹣AE'|=|E'N'﹣AE'|=AE'﹣E'N=AN,再求最大值即可;
(3)设平移后的解析式为y=![]() x+b,当直线经过点P(2,6)时,可得矩形MEGN,再求点G坐标即可.
x+b,当直线经过点P(2,6)时,可得矩形MEGN,再求点G坐标即可.
解:
(1)∵OA=OC,A点坐标为(4,3),
∴OC=5,
∴C(﹣5,0),
将点A(4,3)代入y=![]() 可得k=12,
可得k=12,
∴y=![]() ,
,
将点A(4,3)和C(﹣5,0)代入y=ax+b,可得a=![]() ,b=
,b=![]() ,
,
∴y=![]() x+
x+![]() ;
;
(2)由已知可得,P(2,6),D(0,![]() ),作PK⊥x轴于K,交AC于H,
),作PK⊥x轴于K,交AC于H,
∵HK∥OD,
∴![]() =
=![]() ,
,
∴CD=![]() =
=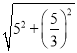 =
=![]()
,
∴![]() =
=![]() ,
,
∴HK=![]() CH,
CH,
∴PH+![]() CH=PH+HK=PK,此时PH+
CH=PH+HK=PK,此时PH+![]() HC为最小,
HC为最小,
∴E与K重合,
∴E(2,0),
如图1中,作B关于x轴的对称点B',B'N∥OE,B'N=OE,连接AN交x轴于E',
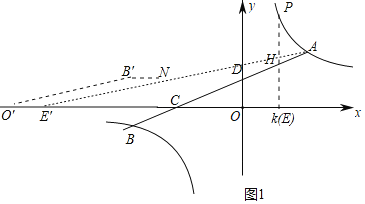
截取E'O'=OE,则B'N∥E'O',B'N=E'O',
∴四边形B'O'E'N是平行四边形,
∴NE'=O'B'=O'B,
∴|BO'﹣AE'|=|E'N'﹣AE'|=AE'﹣E'N=AN,最大;
∵B(﹣9,﹣![]() ),
),
∴B'(﹣9,![]() ),
),
∴N(﹣7,![]() ),
),
∴AN=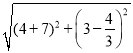 =
=![]() ,
,
∴|BO'﹣AE'|的最大值为![]() ,点E(2,0).
,点E(2,0).
(3)如图3中,
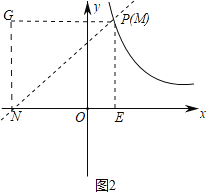
∵直线OA的解析式为y=![]() x,
x,
∴平移后的解析式为y=![]() x+b,
x+b,
当直线经过点P(2,6)时,可得矩形MEGN,
∴6=![]() +b,
+b,
∴b=![]() ,
,
∴平移后的直线的解析式为y=![]() x+
x+![]() ,
,
令y=0,可得x=﹣6,
∴G(﹣6,6).