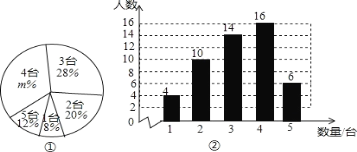
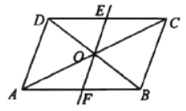
جâؤ؟ؤعبف
،¾جâؤ؟،؟£¨8·ض£©بçح¼£¬شعئ½أوض±½ا×ّ±êدµضذ£¬،÷OABµؤ¶¥µم×ّ±ê·ض±ًخھO£¨0£¬0£©،¢A£¨2£¬1£©،¢B£¨1£¬-2£©£®
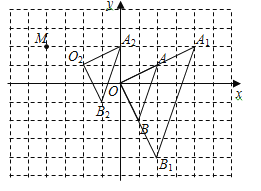
£¨1£©زششµمOخھخ»ثئضذذؤ£¬شعyضلµؤسز²à»³ِ،÷OABµؤز»¸ِخ»ثئ،÷OA1B1 £¬ت¹ثüسë،÷OABµؤدàثئ±بخھ2£؛1£¬²¢·ض±ًذ´³ِµمA،¢Bµؤ¶شس¦µمA1،¢B1µؤ×ّ±ê£®
£¨2£©»³ِ½«،÷OABدٍ×َئ½زئ2¸ِµ¥خ»£¬شظدٍةدئ½زئ1¸ِµ¥خ»؛َµؤ،÷O2A2B2 £¬²¢ذ´³ِµمA،¢Bµؤ¶شس¦µمA2،¢B2µؤ×ّ±ê£®
£¨3£©إذ¶د،÷OA1B1سë،÷O2A2B2 £¬ؤـ·ٌتا¹طسعؤ³ز»µمMخھخ»ثئضذذؤµؤخ»ثئح¼ذخ£¬بôتا£¬اëشعح¼ضذ±ê³ِخ»ثئضذذؤM£¬²¢ذ´³ِµمMµؤ×ّ±ê£®
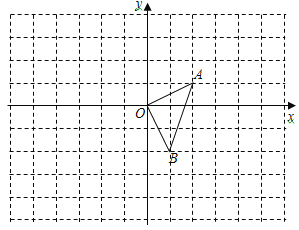
،¾´ً°¸،؟£¨1£©A1£¨4£¬2£©£¬B1£¨2£¬-4£©£» £¨2£©A2£¨0£¬2£©£¬B 2£¨-1£¬-1£©£»£¨3£©،÷OA1B1سë،÷O2A2B2تا¹طسعµمM£¨-4£¬2£©خھخ»ثئضذذؤµؤخ»ثئح¼ذخ£®
،¾½âخِ،؟تشجâ·ضخِ£؛£¨1£©ہûسأخ»ثئح¼ذخµؤذشضتµأ³ِ¶شس¦µم×ّ±ê£¬½ّ¶ّµأ³ِ´ً°¸£»
£¨2£©ہûسأئ½زئ±ن»»¹وآةµأ³ِ¶شس¦µم×ّ±ê£¬½ّ¶ّµأ³ِ´ً°¸£»
£¨3£©ہûسأخ»ثئح¼ذخµؤذشضتµأ³ِخ»ثئضذذؤ£¬½ّ¶ّµأ³ِ´ً°¸£®
تشجâ½âخِ£؛£¨1£©بçح¼ثùت¾£¬A1£¨4£¬2£©£¬B1£¨2£¬-4£© £®
£¨2£©بçح¼ثùت¾£¬A2£¨0£¬2£©£¬B 2£¨-1£¬-1£©£®
£¨3£©،÷OA1B1سë،÷O2A2B2تا¹طسعµمM£¨-4£¬2£©£¬خھخ»ثئضذذؤµؤخ»ثئح¼ذخ£®

 ½ٍاإ½جس¼ئثمذ،×´شھدµءذ´ً°¸
½ٍاإ½جس¼ئثمذ،×´شھدµءذ´ً°¸