题目内容
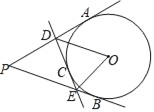
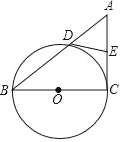
【题目】如图,以△ABC的一边BC为直径作⊙O,交AB于D,E为AC的中点,DE切⊙O于点D.
(1)请判断AC与⊙O的位置关系,并说明理由.
(2)若半径为5,BD为8,求线段AD的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由题意可得:∠ODC=∠OCD,DE=EC,可证∠ODE=∠OCE,由DE是⊙O切线,可得∠ODC=90°,可证∠OCE=90°,则可判断AC与⊙O的位置关系;
(2)由题意可证:△ADC∽△CDB,可得![]() ,即可求AD的长.
,即可求AD的长.
证明:(1)连接CD、DO
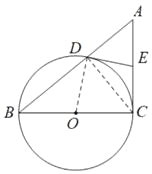
∵BC是直径
∴∠BDC=∠ADC=90°
∵E是中点
∴DE=EC
∴∠EDC=∠ECD
∵OD=OC
∴∠ODC=∠OCD
又 DE切⊙O于点D
∴OD⊥DE
∴∠ODC+∠CDE=90°
∴∠ECD+∠OCD=90°
∴AC⊥OC
∴AC与⊙O相切
(2)∵半径为5
∴BC=10
在Rt△BDC中,BD=8,BC=10
∴CD=6
∵∠ECD+∠OCD=90°,∠OCD+∠B=90°
∴∠ECD=∠B,且∠BDC=∠ADC=90°
∴△ADC∽△CDB
∴![]()
∴![]()
∴AD=![]()

练习册系列答案
相关题目