ĢāÄæÄŚČŻ
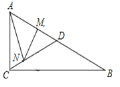
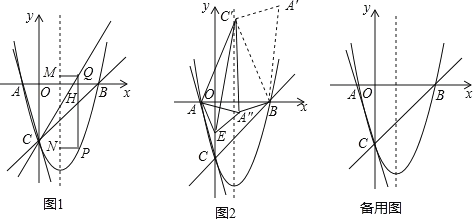
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy![]() ÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£®
ÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£®
£Ø1£©ÅŠ¶Ļ”÷ABCµÄŠĪד£»
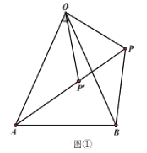
£Ø2£©¹żµćCµÄÖ±Ļßy![]() ½»xÖįÓŚµćH£¬ČōµćPŹĒµŚĖÄĻóĻŽÄŚÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬ĒŅŌŚ¶Ō³ĘÖįµÄÓŅ²ą£¬¹żµćP×÷PQ”ĪyÖį½»Ö±ĻßCHÓŚµćQ£¬×÷PN”ĪxÖį½»¶Ō³ĘÖįÓŚµćN£¬ŅŌPQ”¢PNĪŖĮŚ±ß×÷¾ŲŠĪPQMN£¬µ±¾ŲŠĪPQMNµÄÖܳ¤×ī“óŹ±£¬ŌŚyÖįÉĻÓŠŅ»¶ÆµćK£¬xÖįÉĻÓŠŅ»¶ÆµćT£¬Ņ»¶ÆµćG“ÓĻ߶ĪCPµÄÖŠµćR³ö·¢ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲR”śK”śTµÄĀ·¾¶ŌĖ¶Æµ½µćT£¬ŌŁŃŲĻ߶ĪTBŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æµ½Bµć“¦Ķ£Ö¹ŌĖ¶Æ£¬Ēó¶ÆµćGŌĖ¶ÆµÄ×īÉŁŹ±¼ä¼°“ĖŹ±µćTµÄ×ų±ź£»
½»xÖįÓŚµćH£¬ČōµćPŹĒµŚĖÄĻóĻŽÄŚÅ×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬ĒŅŌŚ¶Ō³ĘÖįµÄÓŅ²ą£¬¹żµćP×÷PQ”ĪyÖį½»Ö±ĻßCHÓŚµćQ£¬×÷PN”ĪxÖį½»¶Ō³ĘÖįÓŚµćN£¬ŅŌPQ”¢PNĪŖĮŚ±ß×÷¾ŲŠĪPQMN£¬µ±¾ŲŠĪPQMNµÄÖܳ¤×ī“óŹ±£¬ŌŚyÖįÉĻÓŠŅ»¶ÆµćK£¬xÖįÉĻÓŠŅ»¶ÆµćT£¬Ņ»¶ÆµćG“ÓĻ߶ĪCPµÄÖŠµćR³ö·¢ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲR”śK”śTµÄĀ·¾¶ŌĖ¶Æµ½µćT£¬ŌŁŃŲĻ߶ĪTBŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æµ½Bµć“¦Ķ£Ö¹ŌĖ¶Æ£¬Ēó¶ÆµćGŌĖ¶ÆµÄ×īÉŁŹ±¼ä¼°“ĖŹ±µćTµÄ×ų±ź£»
£Ø3£©ČēĶ¼2£¬½«”÷ABCČʵćBĖ³Ź±ÕėŠż×ŖÖĮ”÷A'BC'µÄĪ»ÖĆ£¬µćA”¢CµÄ¶ŌÓ¦µć·Ö±šĪŖA'”¢C'£¬ĒŅµćC'Ē”ŗĆĀäŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻ£¬Į¬½ÓAC'£®µćEŹĒyÖįÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓAE”¢C'E£¬½«”÷AC'EŃŲÖ±ĻßC'E·ÕŪĪŖ”÷A”åC'E£¬ŹĒ·ń“ęŌŚµćA'£¬Ź¹µĆ”÷BAA”åĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³öµćEµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©”÷ABCŹĒŅŌACĪŖµ×µÄµČŃüČż½ĒŠĪ£®ĄķÓɼū½āĪö£»£Ø2£©¶ÆµćGŌĖ¶ÆµÄ×īÉŁŹ±¼ät=6![]() Ćė£¬T£Ø
Ćė£¬T£Ø![]() £¬0£©£»£Ø3£©E×ų±źĪŖ£Ø0£¬3
£¬0£©£»£Ø3£©E×ų±źĪŖ£Ø0£¬3![]() £©»ņ£Ø0£¬6£©»ņ£Ø0£¬3
£©»ņ£Ø0£¬6£©»ņ£Ø0£¬3![]() £©»ņ£Ø0£¬12£©£®
£©»ņ£Ø0£¬12£©£®
”¾½āĪö”æ
£Ø1£©½įĀŪ£ŗ”÷ABCŹĒŅŌACĪŖµ×µÄµČŃüČż½ĒŠĪ£¬Ēó³öA£¬B£¬CµÄ×ų±ź£¬Ēó³öBC£¬BA¼“æÉÅŠ¶Ļ£®
£Ø2£©øł¾ŻÖܳ¤µÄ¶ØŅ壬¹¹½Ø¶ž“ĪŗÆŹż£¬Ēó³öÖܳ¤×ī“óŹ±£¬µćP£Ø3![]() £¬-3
£¬-3![]() £©£¬ŅņĪŖRĪŖĻ߶ĪCPµÄÖŠµć£¬ĶĘ³öR£Ø
£©£¬ŅņĪŖRĪŖĻ߶ĪCPµÄÖŠµć£¬ĶĘ³öR£Ø![]() £¬-3
£¬-3![]() £©£¬×÷µćR¹ŲÓŚyÖį¶Ō³ĘµćR”ä£Ø
£©£¬×÷µćR¹ŲÓŚyÖį¶Ō³ĘµćR”ä£Ø![]() £¬-3
£¬-3![]() £©£¬“ĖŹ±RÓėNÖŲŗĻ£¬ÓÉĢāŅāÖŖ£ŗ¶ÆµćGŌĖ¶ÆµÄ×īÉŁŹ±¼ät=RK+KT+
£©£¬“ĖŹ±RÓėNÖŲŗĻ£¬ÓÉĢāŅāÖŖ£ŗ¶ÆµćGŌĖ¶ÆµÄ×īÉŁŹ±¼ät=RK+KT+![]() TB£¬¹żµćR”ä×÷R”äJ”ĶBSÓŚJ£¬½»yÖįÓŚK£¬½»xÖįÓŚT£¬ŌņR”äJ¼“ĪŖĖłĒó£¬ÓÉTJ=
TB£¬¹żµćR”ä×÷R”äJ”ĶBSÓŚJ£¬½»yÖįÓŚK£¬½»xÖįÓŚT£¬ŌņR”äJ¼“ĪŖĖłĒó£¬ÓÉTJ=![]() TB£¬æɵĆt=R”äK+KT+TJ£¬ŌŁĄūÓĆĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒó³öTM¼“æɽā¾öĪŹĢā£®
TB£¬æɵĆt=R”äK+KT+TJ£¬ŌŁĄūÓĆĻąĖĘČż½ĒŠĪµÄŠŌÖŹĒó³öTM¼“æɽā¾öĪŹĢā£®
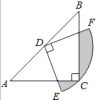
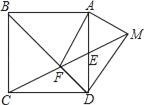
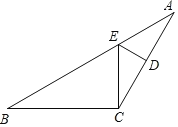
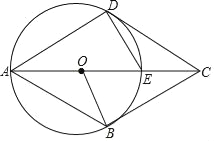
£Ø3£©·ÖĖÄÖÖĒéŠĪ·Ö±š»³öĶ¼ŠĪĒó½ā¼“æÉ£ŗ¢Łµ±AA'=A'BŹ±£¬ČēĶ¼2ÖŠ£®¢Śµ±AA'=ABŹ±£¬ČēĶ¼3ÖŠ£¬ÉčA”åC”ä½»yÖįÓŚJ£®¢Ūµ±AA'=A'BŹ±£¬ČēĶ¼4ÖŠ£¬ÉčAC”ä½»yÖįÓŚM£®¢Üµ±A'B=ABŹ±£¬ČēĶ¼5ÖŠ£®·Ö±šĒó³ö“š°ø¼“æÉ.
½ā£ŗ£Ø1£©”÷ABCŹĒŅŌACĪŖµ×µÄµČŃüČż½ĒŠĪ£®ĄķÓÉČēĻĀ£ŗ
ÓÉĢāŅāÖŖÅ×ĪļĻßy![]() ÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬
ÓėxÖį½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£¬
”ąĮīx=0£¬½āµĆ£ŗy![]() £»Įīx=0£¬½āµĆ£ŗx1
£»Įīx=0£¬½āµĆ£ŗx1![]() £¬x2=4
£¬x2=4![]() £»
£»
”ąA£Ø![]() £¬0£©£¬
£¬0£©£¬![]() £¬
£¬![]() £»
£»
”ąAC2=AM2+MC2![]() 30£¬
30£¬
BC2=OB2+OC2![]() 75£¬
75£¬
AB2=£ØOA+OB£©2![]() 75£¬
75£¬
”ąAB=BC£¬
”ą”÷ABCŹĒŅŌACĪŖµ×µÄµČŃüČż½ĒŠĪ£®
£Ø2£©ČēĶ¼1ÖŠ£¬¹żµćCµÄÖ±Ļßy![]() ½»xÖįÓŚµćH£¬
½»xÖįÓŚµćH£¬

Įīy=0£¬½āµĆ£ŗx![]() £¬
£¬
”ą
ÉčP£Øm£¬![]() 3
3![]() £©£¬ŌņQ£Øm£¬
£©£¬ŌņQ£Øm£¬![]() 3
3![]() £©£®
£©£®
”ßy![]() £¬
£¬
”ąÅ×ĪļĻ߶Ō³ĘÖįĪŖ£ŗÖ±Ļßx![]() £¬
£¬
”ąQP=£Ø![]() 3
3![]() £©©£Ø
£©©£Ø![]() 3
3![]() £©
£©![]() £¬NP=m
£¬NP=m![]() £¬
£¬
”ą¾ŲŠĪPQMNµÄÖܳ¤C¾ŲŠĪPQMN=2£ØQP+NP£©=2£Ø![]() £©
£©![]() £»
£»
”ß![]() 0£¬æŖæŚĻņĻĀ£¬
0£¬æŖæŚĻņĻĀ£¬
”ąµ±m=3![]() Ź±£¬C¾ŲŠĪPQMN×īŠ”£¬“ĖŹ±£¬P£Ø3
Ź±£¬C¾ŲŠĪPQMN×īŠ”£¬“ĖŹ±£¬P£Ø3![]() £¬©3
£¬©3![]() £©£®
£©£®
”ßRĪŖĻ߶ĪCPµÄÖŠµć£¬
”ąR£Ø![]() £¬©3
£¬©3![]() £©£¬×÷µćR¹ŲÓŚyÖį¶Ō³ĘµćR'£Ø
£©£¬×÷µćR¹ŲÓŚyÖį¶Ō³ĘµćR'£Ø![]() £¬©3
£¬©3![]() £©£¬“ĖŹ±RÓėNÖŲŗĻ£¬
£©£¬“ĖŹ±RÓėNÖŲŗĻ£¬
ÓÉĢāŅāÖŖ£ŗ¶ÆµćGŌĖ¶ÆµÄ×īÉŁŹ±¼ät=RK+KT![]() TB£¬
TB£¬
ŌŚyÖįÕż°ėÖįÉĻČ”µćS£Ø0£¬4£©£¬Į¬½ÓÖ±ĻßBS£¬ŌņÖ±ĻßBS½āĪöŹ½ĪŖ£ŗy![]() x+4£¬
x+4£¬
¹żµćR'×÷R'J”ĶBSÓŚJ£¬½»yÖįÓŚK£¬½»xÖįÓŚT£¬ŌņR'J¼“ĪŖĖłĒó£®
”ßtan”ĻSBO![]() £¬
£¬
”ą”ĻSBO=30”ć£¬
”ąTJ![]() TB
TB
¼“t=R'K+KT+TJ£®
”ßRR'=3![]() £¬”ĻRR'J=”ĻBTJ=60”ć£¬
£¬”ĻRR'J=”ĻBTJ=60”ć£¬
”ą”÷KRR'ĪŖµČ±ßČż½ĒŠĪ£¬”ĻRKR'=”ĻKRR'=60”ć£¬
”ą”ĻKRM=”ĻKHR=30”ć£¬
”ąR'J=2RR'=6![]() £»
£»
¼“¶ÆµćGŌĖ¶ÆµÄ×īÉŁŹ±¼ät=6![]() £ØĆė£©£»
£ØĆė£©£»
”ß”÷JMT”×”÷JRR'£¬
”ą![]() £¬¼“
£¬¼“![]() £¬
£¬
”ąTM=3![]() 3£¬
3£¬
”ąT£Ø![]() £¬0£©£»
£¬0£©£»
£Ø3£©¢Łµ±AA'=A'BŹ±£¬ČēĶ¼2ÖŠ£¬

“ĖŹ±£¬A'ŌŚ¶Ō³ĘÖįÉĻ
¶Ō³ĘŠŌæÉÖŖ”ĻAC'E=”ĻA'C'E£¬
ÓÖ”ĻHEC'=”ĻA'C'E£¬
”ą”ĻAC'E=”ĻHEC'£¬
”ąHE=HC'=5![]() £¬
£¬
”ąOE=HE©HO![]() £¬
£¬
”ą![]()
¢Śµ±AA'=ABŹ±£¬ČēĶ¼3ÖŠ£¬ÉčA”åC'½»yÖįÓŚJ£®

“ĖŹ±AA'=AB=BC'=A'C'£¬
”ąĖıߊĪA'ABC'ĪŖĮāŠĪ
ÓɶŌ³ĘŠŌæÉÖŖ£ŗ”ĻAC'E=”ĻA'C'E=30”ć£¬
”ąJE![]() £¬
£¬
”ąOE=OJ©JE=6£¬
”ąE£Ø0£¬6£©£»
¢Ūµ±AA'=A'BŹ±£¬ČēĶ¼4ÖŠ£¬ÉčAC'½»yÖįÓŚM£®

“ĖŹ±£¬A'ŌŚ¶Ō³ĘÖįÉĻ”ĻMC'E=75”ć
ÓÖ”ĻAMO=”ĻEMC'=30”ć£¬
”ą”ĻMEC'=75”ć£¬
”ąME=MC'£¬
”ąMC'![]() £¬
£¬
”ąOE![]() £¬
£¬
”ąE£Ø![]() £©£»
£©£»
¢Üµ±A'B=ABŹ±£¬ČēĶ¼5ÖŠ£¬

“ĖŹ±AC'=A'C'=A'B=AB£¬
”ąĖıߊĪAC'A'BĪŖĮāŠĪ
ÓɶŌ³ĘŠŌæÉÖŖ£¬C'£¬E£¬B¹²Ļߣ¬
”ąOE![]() £¬
£¬
”ąE£Ø0£¬12£©£®
×ŪÉĻĖłŹöæÉµĆ£ŗµćE×ų±źĪŖ£Ø0£¬3![]() £©»ņ£Ø0£¬6£©»ņ£Ø0£¬3
£©»ņ£Ø0£¬6£©»ņ£Ø0£¬3![]() £©»ņ£Ø0£¬12£©£®
£©»ņ£Ø0£¬12£©£®

 ŠĀæĪ±źæģĄÖĢįÓÅŹī¼Ł×÷ŅµÉĀĪ÷ĀĆÓĪ³ö°ęÉēĻµĮŠ“š°ø
ŠĀæĪ±źæģĄÖĢįÓÅŹī¼Ł×÷ŅµÉĀĪ÷ĀĆÓĪ³ö°ęÉēĻµĮŠ“š°ø Źī¼ŁĻĪ½ÓÅąÓŽĢ²ÄÕć½¹¤ÉĢ“óѧ³ö°ęÉēĻµĮŠ“š°ø
Źī¼ŁĻĪ½ÓÅąÓŽĢ²ÄÕć½¹¤ÉĢ“óѧ³ö°ęÉēĻµĮŠ“š°ø