题目内容
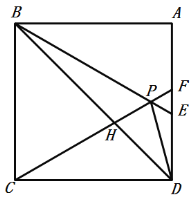
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,点
,点![]() 为边
为边![]() 上的动点,将
上的动点,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,则点
处,则点![]() 到边
到边![]() 距离的最小值是( )
距离的最小值是( )
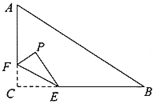
A.3.2B.2C.1.2D.1
【答案】C
【解析】
先依据勾股定理求得AB的长,然后依据翻折的性质可知PF=FC,故此点P在以F为圆心,以2为半径的圆上,依据垂线段最短可知当FP⊥AB时,点P到AB的距离最短,然后依据题意画出图形,最后,利用相似三角形的性质求解即可.
如图所示:当PE∥AB.
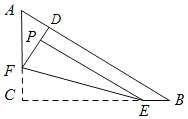
在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
由翻折的性质可知:PF=FC=2,∠FPE=∠C=90°.
∵PE∥AB,
∴∠PDB=90°.
由垂线段最短可知此时FD有最小值.
又∵FP为定值,
∴PD有最小值.
又∵∠A=∠A,∠ACB=∠ADF,
∴△AFD∽△ABC.
∴![]() ,即
,即![]() ,解得:DF=3.2.
,解得:DF=3.2.
∴PD=DF-FP=3.2-2=1.2.
故选:C.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案【题目】某学校八、九两个年级各有学生180人,为了解这两个年级学生的体质健康情况,进行了抽样调查,具体过程如下:
收集数据
从八、九两个年级各随机抽取20名学生进行体质健康测试,测试成绩(百分制)如下:
八年级 | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
九年级 | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
整理、描述数据
将成绩按如下分段整理、描述这两组样本数据:
成绩(x) | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
八年级人数 | 0 | 0 | 1 | 11 | 7 | 1 |
九年级人数 | 1 | 0 | 0 | 7 | 10 | 2 |
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如表所示:
年级 | 平均数 | 中位数 | 众数 | 方差 |
八年级 | 78.3 | 77.5 | 75 | 33.6 |
九年级 | 78 | 80.5 | a | 52.1 |
(1)表格中a的值为______;
(2)请你估计该校九年级体质健康优秀的学生人数为多少?
(3)根据以上信息,你认为哪个年级学生的体质健康情况更好一些?请说明理由.(请从两个不同的角度说明推断的合理性)
【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
线路 公交车用时的频数 公交车用时 | 30<t ≤35 | 35<t ≤40 | 40<t ≤45 | 45<t ≤50 | 合计 |
A | 59 | 151 | a | 124 | 500 |
B | 50 | b | 122 | 278 | 500 |
C | 45 | 265 | 167 | c | 500 |
(1)将上面表格补充完整;
(2)某天王先生和李女士从甲地到乙地,试用树状图或列表法求在早高峰期间两人刚好乘坐同一条线路的概率;
(3)小张从甲地到乙地,早高峰期间用时不超过45分钟,请问小张应该选择哪条线路?请说明理由.