Question

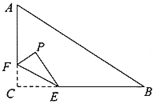
【题目】如图，在正方形中，以为边作等边，延长分别交于点，连接与相交于点，给出下列结论： ①；②；③；④；其中正确的是（ ）

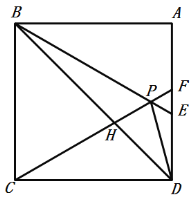
A.①②③④B.②③C.①②④D.①③④

Answer 1

【答案】A

【解析】

根据等边三角形、正方形的性质求得∠ABE=30°，利用直角三角形中30°角的性质即可判断①；证得PC=CD，利用三角形内角和定理即可求得∠PDC，可求得∠BPD，即可判断②；求得∠FDP=15°，∠PBD=15°，即可证明△PDE∽△DBE，判断③正确；利用相似三角形对应边成比例可判断④．

∵△BPC是等边三角形，
∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°，
在正方形ABCD中，
∵AB=BC=CD，∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°，

∴，
∴；故①正确；
∵PC=CD，∠PCD=30°，
∴∠PDC=∠CPD ===75°，

∴∠BPD=∠BPC+ ∠CPD =60°+75°=135°，故②正确；
∵∠PDC=75°，

∴∠FDP=∠ADC -∠PDC=90°- 75°=15°，
∵∠DBA=45°，
∴∠PBD=∠DBA -∠ABE =45°-30°=15°，
∴∠EDP=∠EBD，
∵∠DEP=∠DEP，
∴△PDE∽△DBE，故③正确；
∵△PDE∽△DBE，

∴，即，故④正确；

综上：①②③④都是正确的．
故选：A．