题目内容
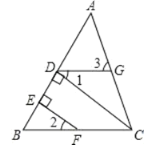
【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.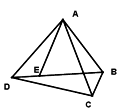
①试说明BE·AD=CD·AE;
②根据图形特点,猜想 ![]() 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
【答案】解:①∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠DAC=∠BAE,
∵∠AEB=∠ADB+∠DAE,
∠ADC=∠ADB+∠BDC,
又∵∠DAE=∠BDC,
∴∠AEB=∠ADC,
∴△BEA∽△CDA,
∴ ![]() =
= ![]() ,
,
即BE·AD=CD·AE;
②猜想 ![]() =
= ![]() 或(
或( ![]() ),
),
由△BEA∽△CDA可知, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
又∵∠DAE=∠BAC,
∴△BAC∽△EAD,
∴ ![]() =
= ![]() 或(
或( ![]() )
)
【解析】①根据∠BAC=∠DAE证明∠DAC=∠BAE,再根据三角形的外角性质得出∠AEB=∠ADB+∠DAE,∠ADC=∠ADB+∠BDC,由∠BDC=∠DAE,证出∠AEB=∠ADC,然后根据两组角对应相等的两三角形相似,得对应边成比例,即可证得结论。
(2)根据已知证明△BEA∽△CDA和△BAC∽△EAD,即可得出结论。
【考点精析】利用三角形的外角和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
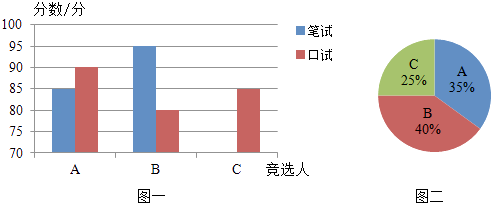
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.