题目内容
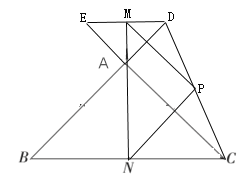
【题目】定义：既相等又垂直的两条线段称为“等垂线段”，如图1，在
中，
，
，点
、
分别在边
、
上，
，连接
、
，点
、
、
分别为、、
的中点，且连接
、
．
观察猜想
（1）线段与 “等垂线段”（填“是”或“不是”）
猜想论证
（2）
绕点
按逆时针方向旋转到图2所示的位置，连接
，
，试判断与是否为“等垂线段”，并说明理由．
拓展延伸
（3）把
绕点在平面内自由旋转，若
，
，请直接写出与的积的最大值．
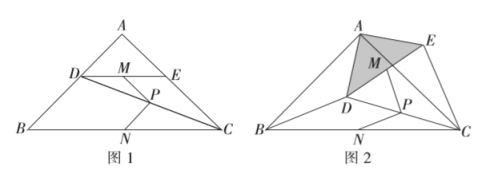
【答案】（1）是；（2）是，理由详见解析；（3）49
【解析】
（1）根据题意，利用等腰三角形和三角形中位线定理得出
，∠MPN=90°判定即可；
（2）由旋转和三角形中位线的性质得出，再由中位线定理进行等角转换，得出∠MPN=90°，即可判定；
（3）由题意，得出
最大时，
与
的积最大，点
在
的延长线上，再由（1）（2）结论，
得出与的积的最大值.
（1）是；
∵
，
∴DB=EC，∠ADE=∠AED=∠B=∠ACB
∴DE∥BC
∴∠EDC=∠DCB
∵点
、
、
分别为
、
、
的中点
∴PM∥EC，PN∥BD，
∴，∠DPM=∠DCE，∠PNC=∠DBC
∵∠DPN=∠PNC+∠DCB
∴∠MPN=∠DPM+∠DPN=∠ACD+∠DCB+∠B=180°-90°=90°
∴线段与是“等垂线段”；
（2）由旋转知
∵，
∴
≌
（
）
∴
，
利用三角形的中位线得
，
，
∴
由中位线定理可得
，
∴
，
∵
∴
∵
∴
∴
∴与为“等垂线段”；
（3）与的积的最大值为49；
由（1）（2）知，
∴最大时，与的积最大
∴点在的延长线上，如图所示：
∴
∴
∴
.
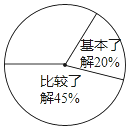
【题目】某校开展了主题为“梅山文化知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，整理调查数据制成了不完整的表格和扇形统计图（如图）．
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题：
（1）本次问卷调查共抽取的学生数为多少人，表中m的值为多少；
（2）计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数，并补全扇形统计图；
（3）若该校有学生2000人，请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少？
【题目】王勇和李明两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了30次实验，实验的结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
（1）分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率；
（2）王勇说：“根据以上实验可以得出结论：由于5点朝上的频率最大，所以一次实验中出现5点朝上的概率最大”；李明说：“如果投掷300次，那么出现6点朝上的次数正好是30次”．试分别说明王勇和李明的说法正确吗？并简述理由；
（3）现王勇和李明各投掷一枚骰子，请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
