题目内容
【题目】如图,正方形ABCD与正方形EFGH是位似形,已知A(0,5),D(0,3),E(0,1),H(0,4),则位似中心的坐标是 . 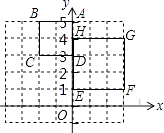
【答案】(0,![]() ),(﹣6,7)
),(﹣6,7)
【解析】解:设当B与F是对应点, 
设直线BF的解析式为:y=kx+b,
则 ![]() ,
,
解得:  ,
,
故直线BF的解析式为:y=﹣ ![]() x+
x+ ![]() ,
,
则x=0时,y= ![]() ,
,
即位似中心是:(0, ![]() ),
),
设当C与E是对应点,设直线CE的解析式为:y=ax+c,
则 ![]() ,
,
解得: ![]() ,
,
故直线CE的解析式为:y=﹣x+1,
设直线DF的解析式为:y=dx+e,
则 ![]() ,
,
解得:  ,
,
故直线DF的解析式为:y=﹣ ![]() x+3,
x+3,
则  ,
,
解得: ![]()
即位似中心是:(﹣6,7),
综上所述:所述位似中心为:(0, ![]() ),(﹣6,7).
),(﹣6,7).
故答案为:(0, ![]() ),(﹣6,7).
),(﹣6,7).
根据如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,对应边互相平行或在一条直线上,那么这两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比; 性质: 位似图形的对应点和位似中心在同一直线上,它们到位似中心的距离之比等于相似比;位似多边形的对应边平行或共线; 设当B与F是对应点,求出直线BF的解析式 ,得到位似中心是点(0, ![]() );设当C与E是对应点,求出直线CE的解析式;求出直线DF的解析式,得到位似中心是点(﹣6,7),综上所述求出位似中心的坐标.
);设当C与E是对应点,求出直线CE的解析式;求出直线DF的解析式,得到位似中心是点(﹣6,7),综上所述求出位似中心的坐标.

【题目】一辆汽车在公路上行驶,其所走的路程和所用的时间可用下表表示:
时间t(min) | 1 | 2.5 | 5 | 10 | 20 | 50 | … |
路程s(km) | 2 | 5 | 10 | 20 | 40 | 100 | … |
(1)在这个变化过程中,自变量、因变量各是什么?
(2)当汽车行驶的路程为20 km时,所花的时间是多少分钟?
(3)随着t逐渐变大,s的变化趋势是什么?
(4)路程s与时间t之间的函数表达式为______________.
(5)按照这一行驶规律,当所花的时间t是300 min时,汽车行驶的路程s是多少千米?