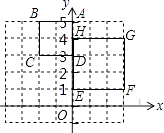题目内容
【题目】以数轴上的原点O为圆心，3为半径的扇形中，圆心角∠AOB=90°，另一个扇形是以点P为圆心，5为半径，圆心角∠CPD=60°，点P在数轴上表示实数a，如图．如果两个扇形的圆弧部分（ 
和 
）相交，那么实数a的取值范围是 ． 
【答案】﹣4≤a≤﹣2
【解析】解：当A、D两点重合时，PO=PD﹣OD=5﹣3=2，此时P点坐标为a=﹣2，
当B在弧CD时，由勾股定理得，PO= 
= 
=4，此时P点坐标为a=﹣4，
则实数a的取值范围是﹣4≤a≤﹣2．
所以答案是：﹣4≤a≤﹣2．
【考点精析】解答此题的关键在于理解圆与圆的位置关系的相关知识，掌握两圆之间有五种位置关系：无公共点的，一圆在另一圆之外叫外离，在之内叫内含；有唯一公共点的，一圆在另一圆之外叫外切，在之内叫内切；有两个公共点的叫相交．两圆圆心之间的距离叫做圆心距．两圆的半径分别为R和r，且R≥r，圆心距为P：外离P＞R+r；外切P=R+r；相交R-r＜P＜R+r；内切P=R-r；内含P＜R-r．，以及对实数与数轴的关系的理解，了解实数与数轴上的点一一对应．
【题目】为了了解江城中学学生的身高情况，随机对该校男生、女生的身高进行抽样调查，已知抽取的样本中，男生、女生的人数相同，根据所得数据绘制成如下所示的统计表和如图所示的统计图．
组别 | 身高(cm) |
A | x<150 |
B | 150≤x＜155 |
C | 155≤x＜160 |
D | 160≤x＜165 |
E | x≥165 |
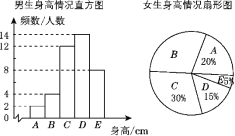
根据图表中提供的信息，回答下列问题：
(1)女生身高在B组的有________人；
(2)在样本中，身高在150≤x＜155之间的共有________人，身高人数最多的在________组(填组别序号)；
(3)已知该校共有男生500人，女生480人，请估计身高在155≤x＜165之间的学生有多少人．
