题目内容
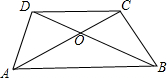
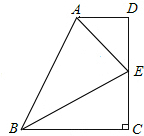
已知四边形ABCD的对角线AC、BD相交于点O,下列条件中能够判断有一组对边平行的是( )
| A.AD:BC=AO:CO | B.AD:BC=DO:CO |
| C.AO:BO=CO:DO | D.AO:BO=DO:CO |
相似三角形的判定定理之一是:两边对应成比例,且夹角相等的两个三角形相似,
A、根据AD:BC=AO:CO,不具备夹角相等,即不能推出两三角形相似,即不能得逞两内错角相等,根据平行线的判定不能推出两边平行,故本选项错误;
B、根据AD:BC=DO:CO,不具备夹角相等,即不能推出两三角形相似,即不能得逞两内错角相等,根据平行线的判定不能推出两边平行,故本选项错误;
C、∵AO:OB=CO:DO,
∴
| AO |
| CO |
| BO |
| DO |
∵∠AOB=∠COD,
∴△AOB∽△COD,
∴∠BAC=∠DCA,
∴AB∥CD,故本选项正确;
D、∵AO:BO=DO:CO,∠AOD=∠COB,
∴△AOD∽△BOC,
∴∠DAO=∠CBO,∠ADO=∠BCO,
∴不能推出AD∥BC或AB∥CD,故本选项错误;
故选C.


练习册系列答案
相关题目