题目内容
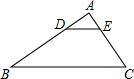
如图，在梯形ABCD中AB∥CD，对角线AC、BD交于点O，若CD=2，AB=5，则S△BOC：S△ADC=______．
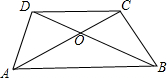
∵AB∥CD，∴△AOB∽△COD，
设△AOB的高为h1，△COD的高为h2，则
=
=
，
∴S△BCD：S△ODC=（h1+h2）：h2=7：2，
∴S△BCD：S△BOC=7：5，又∵S△BDC=S△ADC，
∴S△BOC：S△ADC=5：7．
设△AOB的高为h1，△COD的高为h2，则
| h1 |
| h2 |
| AB |
| CD |
| 5 |
| 2 |
∴S△BCD：S△ODC=（h1+h2）：h2=7：2，
∴S△BCD：S△BOC=7：5，又∵S△BDC=S△ADC，
∴S△BOC：S△ADC=5：7．
练习册系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
