题目内容
如图所示.直角梯形ABCD中,∠C=90°,AD∥BC,AD+BC=AB,E是CD的中点.若AD=2,BC=8,求△ABE的面积.
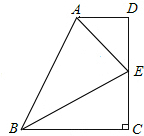

取AB中点F,连接EF.由梯形中位线性质知EF∥AD,
过A作AG⊥BC于G,交EF于H.由平行线等分线段定理知,AH=GH且AH,GH均垂直于EF.
在Rt△ABG中,由勾股定理知:AG2=AB2-BG2
=(AD+BC)2-(BC-AD)2
=102-62=82,
∴AG=8,
从而AH=GH=4,
∴S△ABE=S△AEF+S△BEF
=
EF•AH+
EF•GH=
EF•(AH+GH)=
EF•AG
=
×5×8=20.

过A作AG⊥BC于G,交EF于H.由平行线等分线段定理知,AH=GH且AH,GH均垂直于EF.
在Rt△ABG中,由勾股定理知:AG2=AB2-BG2
=(AD+BC)2-(BC-AD)2
=102-62=82,
∴AG=8,
从而AH=GH=4,
∴S△ABE=S△AEF+S△BEF
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目