题目内容
【题目】观察一列数：1、2、4、8、16、32、…，发现从第二项开始，每一项与前一项的比值都是同一个常数，这个常数是_______；根据此规律，如果
(
为正整数)表示这个数列的第项，如果
，
，那么
_____，…，
_______；
如果欲求
的值，
可令
…………①
将①式两边同乘以2，得
……………②
由②减去①式，得
.
(2)类比可得：
__________.
(3)用由特殊到一般的方法知：若数列
、
、
、…、，从第二项开始每一项与前一项之比的常数为
，那么
，____，…，______ (用含，
，的代数式表示).
用含，，的代数式表示
_________.
(4)一质点从距离原点一个单位的A点向原点方向跳动，第一次跳到OA中点
处，第二次从跳到
的中点
处，第三次从跳到
的中点
处，…，如此不断跳下去，则第50次跳动后，该质点跳动的距离是多少？
【答案】(1) 这个常数是2，
；
；(2)
；(3)
；
；
；(4)该质点跳动的距离是
.
【解析】
（1）根据题意，可得在这个数列中，从第二项开始，每一项与前一项之比是2；有第一个数为2，故可得a18，an的值；
（2）根据题中的提示，可得S的值；
（3）由（2）的方法，依次可以推出a1+a2+a3+…+an的值.
（4）由已知条件求出首项和公比，再代入等比数列前n项和公式的答案．
(1) 这个常数是2，；
(2) 令
…………①
将①式两边同乘以5，得
……………②
由②减去①式，得
.
.
故答案为：
(3)；
；
, ①
, ②
由②减去①式，得
.
.
(4)
,
.
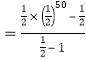答：该质点跳动的距离是
.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
