题目内容
3.同时抛掷A、B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两个立方体朝上的数字分别为x、y,并以此确定点P(x,y),那么点P落在抛物线y=-x2+3x上的概率为( )| A. | $\frac{1}{18}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
分析 画树状图展示所有36种等可能的结果数,再根据二次函数图象上点的坐标特征得到点(1,2),(2,2)在抛物线y=-x2+3x上,然后根据概率公式求解.
解答 解:画树状图为:
共有36种等可能的结果数,其中点(1,2),(2,2)在抛物线y=-x2+3x上,
所以点P在抛物线y=-x2+3x上的概率=$\frac{2}{36}$=$\frac{1}{18}$.
故选A.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.a、b两数的平方和用代数式表示( )
| A. | (a+b)2 | B. | (a-b)2 | C. | a3+b3 | D. | a2+b2 |
14. 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )| A. | 点C | B. | 点D | C. | 点A | D. | 点B |
 如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+12与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.
如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+12与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M. 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,连PD,下列结论:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正确的结论是( )
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,连PD,下列结论:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正确的结论是( )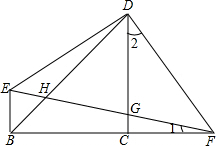 如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,
如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上, 如图,在⊙O中,OA、OB是半径,OA⊥OB,C、D是$\widehat{AB}$的三等分点,OC、OD分别交AB于点E、F,求证:AE=CD=BF.
如图,在⊙O中,OA、OB是半径,OA⊥OB,C、D是$\widehat{AB}$的三等分点,OC、OD分别交AB于点E、F,求证:AE=CD=BF.