题目内容
【题目】如图,M为正方形ABCD边AB的中点,E是AB延长线上的一点,MN⊥DM,且交∠CBE的平分线于N.
(1)求证:MD=MN;
(2)若将上述条件中的“M为AB边的中点”改为“M为AB边上任意一点”,其余条件不变,则结论“MD=MN”成立吗?如果成立,请证明;如果不成立,说明理由.

【答案】(1)详见解析;(2)成立,理由详见解析.
【解析】
(1)要证MD=MN,就要构建△DFM≌△MBN,只需取AD的中点F,连接FM,依据正方形的性质可证
(2)只需作AF=AM,其余证法与1同.
解:(1)证明:取AD的中点F,连接MF.
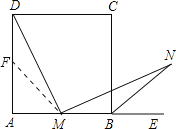
∵四边形ABCD是正方形,M是AB的中点,
∴∠A=∠ABC=90°,DF=AF=AM=MB,
∴∠AFM=45°.
又∵BN平分∠CBE,
∴∠EBN=45°,
∴∠EBN=∠AFM,
∴∠DFM=∠MBN.
又∵∠FDM+∠DMA=90°,
∠BMN+∠DMA=90°,
∴∠FDM=∠BMN,
∴△FDM≌△BMN,∴MD=NM.
(2)结论“MD=NM”仍然成立.
理由:与(1)类似,在AD上截取DF=MB,连接M.
易得∠FDM=∠BMN,∠DFM=∠MBN,
从而△FDM≌△BMN,∴MD=NM.

练习册系列答案
相关题目