Question

【题目】如图，在△ABC中， BD是∠ABC的平分线，过点C作CE⊥BD，交 BD的延长线于点E，∠ABC=60°，∠ECD=15°.

(1)直接写出∠ADB的度数是_______；

(2)求证：BD=AB；

(3)若AB=2，求BC的长．

Answer 1

【答案】（1）75°；（2）证明见解析；（3）BC=.

【解析】

（1）先求出∠EDC的度数，从而求出∠EDC的对顶角∠ADB；

（2）根据条件求出∠ADB=75°，得出∠A=75°，随之即可解答.

（3）过点D作DF⊥BC，交BC于F点，根据条件求出FB，FC的长度即可解答.

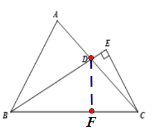
（1）75°

∠EDC=90°－∠ECD=75°，∴∠ADB=∠EDC=75°.

（2）证明：∵BD平分∠ABC

∠ABC=60°

∴∠ABD=∠DBC=30°

∵∠ADB=75°

∴∠A=75°

∴∠A=∠ADB

∴AB=DB

（3）过点D作DF⊥BC，交BC于F点

∵DF⊥BC

∴∠DFB=∠DFC=90°

∵∠DBF=30°

∴DF=BD

∵BD=AB=2

∴DF =1

∴FB=

∵CE⊥BE

∴∠E=90°

∵∠DBC=30°

∴∠ECB=60°

∵∠ECD=15°

∴∠DCB=45°

∴∠DCF=∠FDC=45°

∴FC= FD=1

∴BC=