题目内容
【题目】已知:在△ABC中,AH⊥BC,垂足为点H,若AB+BH=CH,∠ABH=70°,则∠BAC=_____°.
【答案】75°或35°
【解析】
分析题意,可知本题需分两种情况进行讨论,△ABC为锐角三角形和△ABC为直角三角形;
当△ABC为钝角三角形时,过A作BC的垂线,交CB的延长线于点H,由AB+BH=CH,不难得出AB=BC,接下来,再利用三角形外角的性质,可得∠BAC的度数;
当△ABC为锐角三角形时,在HC上取D点,使BH=HD,连接AD,再结合AB+BH=CH,不难得出AD=DC,接下来,再利用三角形外角的性质,可得∠DAC的度数;
由∠ABH=70°,利用等腰三角形的性质可得出∠BAD的度数,结合上述所得,可得∠BAC的度数.
根据题意画出图形,
当△ABC为钝角三角形时,过A作BC的垂线,交CB的延长线于点H,
∵AB+BH=CH,HB+BC=CH,
∴AB=BC,
∴∠BAC=∠ACB.
∵∠ABH=70°,
∴∠BAC=∠ACB=35°.
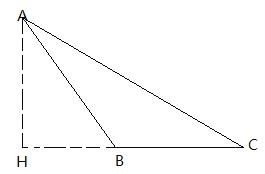
当△ABC为锐角三角形时,在HC上取D点,使BH=HD,连接AD,
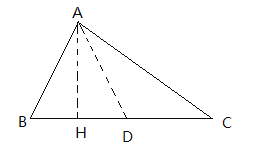
∵AB+BH=HC=HD+DC,BH=HD,
∴AB=DC.
∵AH⊥BD,BH=HD,
∴AB=AD,
∴∠B=∠ADH=70°,
∴∠BAD=40°.
∵AB=DC,AB=AD,
∴AD=CD,
∴∠C=∠DAC,
∴∠ADH=∠C+∠DAC=2∠C,
∴∠DAC=35°,
∴∠BAC=∠BAD+∠DAC=40°+35°=75°.
故答案为:75°或35°

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目