题目内容
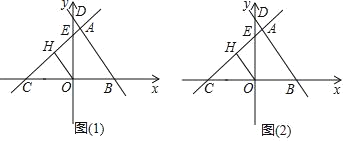
【题目】如图(1),平面直角坐标系中,直线y=![]() 与x轴、y轴分别交于点B、D,直线y=
与x轴、y轴分别交于点B、D,直线y=![]() 与x轴、y轴分别交于点C、E,且两条直线交于点A.
与x轴、y轴分别交于点C、E,且两条直线交于点A.
(1)若OH⊥CE于点H,求OH的长.
(2)求四边形ABOE的面积.
(3)如图(2),已知点F(﹣![]() ,0),在△ABC的边上取两点M、N,是否存在以点O,M,N为顶点的三角形与△OFM全等,且两个三角形在边OM的异侧?若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.(温馨提示:若点A(x1,y1),点B(x2,y2),则线段AB的中点坐标为(
,0),在△ABC的边上取两点M、N,是否存在以点O,M,N为顶点的三角形与△OFM全等,且两个三角形在边OM的异侧?若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.(温馨提示:若点A(x1,y1),点B(x2,y2),则线段AB的中点坐标为(![]() ,
,![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)满足条件的点M坐标为(﹣
;(3)满足条件的点M坐标为(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() )或(0,3).
)或(0,3).
【解析】
(1)利用面积法:![]() ×CE×OH=
×CE×OH=![]() ×OC×OA即可解决问题;
×OC×OA即可解决问题;
(2)求出A、E、B、A的坐标,利用分割法即可解决问题;
(3)分四种情形分别求解即可解决问题.
(1)∵直线y=![]() 与x轴、y轴分别交于点C、E,
与x轴、y轴分别交于点C、E,
∴C(﹣4,0),E(0,3),
∴OC=4,OE=3,
∴EC=![]() ,
,
∵OH⊥CE,
∴![]() ×CE×OH=
×CE×OH=![]() ×OC×OA,
×OC×OA,
∴OH=![]() =
=![]() .
.
(2)如图1中,连接OA.
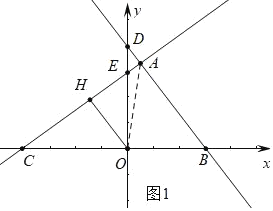
∵直线y=![]() 与x轴、y轴分别交于点B、D,
与x轴、y轴分别交于点B、D,
∴D(0,4),B(3,0),
由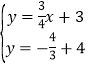 ,解得
,解得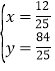 ,
,
∴A(![]() ,
,![]() ),
),
∴S四边形ABOE=S△AOE+S△AOB=![]() ×3×
×3×![]() +
+![]() ×4×
×4×![]() =
=![]() .
.
(3)①如图2中,当FM⊥OC时,△OMN≌△OMF.
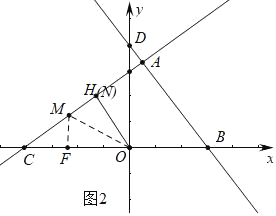
∵F(﹣![]() ,0),OH=
,0),OH=![]() ,
,
∴OF=OH,
∴当FM⊥OC时,△OMN≌△OMF,
此时M(﹣![]() ,
,![]() ).
).
②如图3中,作ON⊥AB于N,易知N(![]() ,
,![]() ),ON=OF,当OM平分∠CON时,△OMN≌△OMF.
),ON=OF,当OM平分∠CON时,△OMN≌△OMF.
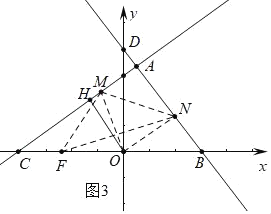
设M(m,![]() m+3),由MF=MN,可得:(m+
m+3),由MF=MN,可得:(m+![]() )2+(
)2+(![]() m+3)2=(m﹣
m+3)2=(m﹣![]() )2+(
)2+(![]() )2,
)2,
解得m=﹣![]() ,
,
∴M(﹣![]() ,
,![]() ).
).
③如图4中,当MN∥OF,且MN=OF时,△OFM≌△MNO.
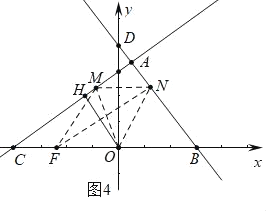
设M(x,![]() x+3),则N(x+
x+3),则N(x+![]() ,﹣
,﹣![]() (x+
(x+![]() )+4),
)+4),
∴![]() x+3=﹣
x+3=﹣![]() (x+
(x+![]() )+4,
)+4,
解得x=﹣![]() ,
,
∴M(﹣![]() ,
,![]() ).
).
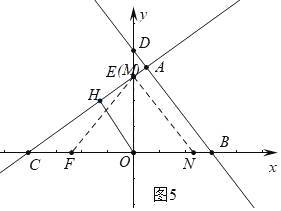
④如图5中,当点M与E重合,且OF=ON时,△OMF≌△OMN,此时M(0,3).
综上所述,满足条件的点M坐标为(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() )或(0,3).
)或(0,3).

 阅读快车系列答案
阅读快车系列答案