题目内容
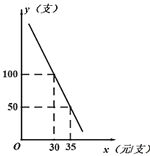
【题目】某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)请求出y与x的函数关系式;
(2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出 200 元捐赠给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定该款电动牙刷的售单价?
【答案】(1)y=-10x+400;(2)单价定为30元时,每天销售利润最大,最大销售利润为1000元;(3)销售单价每支不低于25元,且不高于35元时,可保证捐款后每天剩余利润不低于550元.
【解析】
(1)利用待定系数法将(30,100),(35,50)代入可得函数关系式;
(2)根据利润=单件利润×销售量,列出函数关系式并配方可得最值;
(3)画出函数的大致图象,当W=550时x=25或35,知25≤x≤35时,W≥550.
(1)设y与x的函数关系式为y=kx+b,
将(30,100),(35,50)代入y=kx+b,得![]() ,
,
解得![]() ,
,
∴y与x的函数关系式为y=-10x+400;
(2)设该款电动牙刷每天的销售利润为w元,
由题意得 w=(x-20)·y=(x-20)(-10x+400)=-10x2+600x-8000 =-10(x-30)2 +1000,
∵-10<0,
∴当x=30时,w有最大值,w最大值为1000.
答:该款电动牙刷销售单价定为30元时,每天销售利润最大,最大销售利润为1000元;
(3)设捐款后每天剩余利润为 z 元,
由题意可得z=-10x2+600x-8000-200 =-20x2+600x-8200,
令z=550,
即-10x2+600x-8200=550,
解得x1=25,x2=35,
画出每天剩余利润z关于销售单价x的函数关系图象如解图,
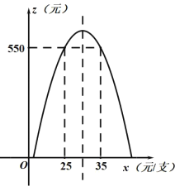
由图象可得:当该款电动牙刷的销售单价每支不低于25元,且不高于35元时,可保证捐款后每天剩余利润不低于550元.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案