Question

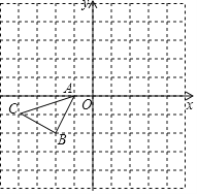
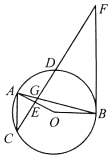
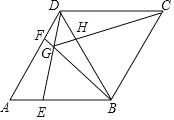
【题目】如图，在菱形ABCD中，AB＝BD，点E、F分别是线段AB、AD上的动点（不与端点重合），且AE＝DF，BF与DE相交于点G．给出如下几个结论：①△AED≌△DFB；②∠BGE大小会发生变化；③CG平分∠BGD；④若AF＝2DF，则BG＝6GF；．其中正确的结论有_____（填序号）．

Answer 1

【答案】①③④．

【解析】

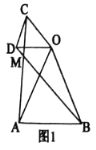
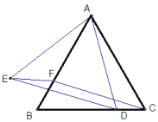
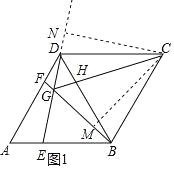
根据菱形的性质得到AB＝AD，推出△ABD为等边三角形，得到∠A＝∠BDF＝60°，根据全等三角形的判定得到△AED≌△DFB；过点C作CM⊥GB于M，CN⊥GD于N（如图1），根据全等三角形的性质得到CN＝CM，根据角平分线的定义得到CG平分∠BGD；过点F作FP∥AE交DE于P点（如图2），根据平行线分线段成比例定理得到BG＝6GF；推出B、C、D、G四点共圆，根据圆周角定理得到∠BGC＝∠BDC＝60°，∠DGC＝∠DBC＝60°，求得∠BGC＝∠DGC＝60°，过点C作CM⊥GB于M，CN⊥GD于N（如图1），推出S四边形BCDG＝S四边形CMGN，于是得到S四边形CMGN＝2S△CMG＝2××CG×CG＝CG2．

解：①∵ABCD为菱形，

∴AB＝AD，

∵AB＝BD，∴△ABD为等边三角形，

∴∠A＝∠BDF＝60°，

又∵AE＝DF，AD＝BD，

∴△AED≌△DFB（SAS），故本选项①正确；

②∵∠BGE＝∠BDG+∠DBF＝∠BDG+∠GDF＝60°，为定值，

故本选项②错误；

③过点C作CM⊥GB于M，CN⊥GD于N（如图1），

则△CBM≌△CDN（AAS），

∴CN＝CM，

∵CG＝CG，

∴Rt△CNG≌Rt△CMG（HL），

∴∠DGC＝∠BGC，

∴CG平分∠BGD；故本选项③正确；

④过点F作FP∥AE交DE于P点（如图2），

∵AF＝2FD，

∴FP：AE＝DF：DA＝1：3，

∵AE＝DF，AB＝AD，

∴BE＝2AE，

∴FP：BE＝FP：2AE＝1：6，

∵FP∥AE，

∴PF∥BE，

∴FG：BG＝FP：BE＝1：6，

即BG＝6GF，故本选项④正确；

⑤∵∠BGE＝∠BDG+∠DBF＝∠BDG+∠GDF＝60°＝∠BCD，

即∠BGD+∠BCD＝180°，

∴点B、C、D、G四点共圆，

∴∠BGC＝∠BDC＝60°，∠DGC＝∠DBC＝60°，

∴∠BGC＝∠DGC＝60°，

过点C作CM⊥GB于M，CN⊥GD于N（如图1），

则△CBM≌△CDN（AAS），

∴S四边形BCDG＝S四边形CMGN，

S四边形CMGN＝2S△CMG，

∵∠CGM＝60°，

∴GM＝CG，CM＝CG，

∴S四边形CMGN＝2S△CMG＝2××CG×CG＝CG2，故本选项⑤错误；

综上所述，正确的结论有①③④，共3个，

故答案为①③④．